题目内容
已知：
，当
时，
；
时，
（1）求
的解析式
（2）c为何值时，
的解集为R.
⑴
⑵
解析试题分析：⑴由时，；时，
知：
是是方程
的两根
⑵由
，知二次函数
的图象开口向下
要使
的解集为R，只需
即
∴当时的解集为R.
考点：本题考查了函数的解析式及恒成立问题
点评：涉及到二次函数的恒成立问题往往需要用到：（1）若二次函数y=a
+bx+c(a≠0)大于0恒成立，则有
，（2）若是二次函数在指定区间上的恒成立问题，可以利用韦达定理以及根的分布知识求解。
练习册系列答案
相关题目
在
处有极大值7．
的解析式；(Ⅱ)求
=1处的切线方程．
，
.
在点
处的切线方程；
在区间
上均为增函数,求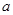
的取值范围；
有唯一解,试求实数
的值. 
（
）是定义在
上的奇函数，且
时，函数
取极值1．
，若
（
），不等式
恒成立，求实数
的取值范围；
,
的单调区间；
，且
，有
，求实数
的取值范围.
（
）的图象如图．根据图象写出：
的
值．
（
）是偶函数
的值；
，若函数
与
的图像有且只有一个公共点，求实数
的取值范围
，证明函数
在
上单调递增；
.