题目内容
设R,r分别为Rt△的外接圆半径和内切圆半径,则| γ | R |
分析:用三角形的三边表示出两个圆的半径,用基本不等式求最值即可.
解答:解:设三角形三边为a,b,c,其中c为三角形的斜边,则R=
c
由面积公式得
r(a+b+c)=
ab
∴r=
=
≤
①
等号当且仅当a=b时取等号,所以三角形为等腰直角三角形
所以a=b=
c 代入①
得r≤
所以则
的最大值为
故应填
| 1 |
| 2 |
由面积公式得
| 1 |
| 2 |
| 1 |
| 2 |
∴r=
| ab |
| a+b+c |
| ab | ||
a+b+
|
| ab | ||||
2
|
等号当且仅当a=b时取等号,所以三角形为等腰直角三角形
所以a=b=
| ||
| 2 |
得r≤
| ||
4+2
|
所以则
| γ |
| R |
| ||
2+
|
故应填
| ||
2+
|
点评:考查基本不等式求最值以及三角形的面积公式的两种形式

练习册系列答案
相关题目
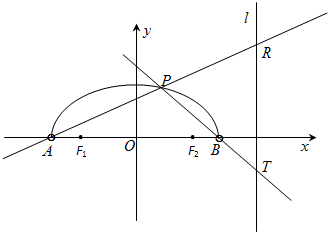 如图,在x轴上方有一段曲线弧Γ,其端点A、B在x轴上(但不属于Γ),对Γ上任一点P及点F1(-1,0),F2(1,0),满足:
如图,在x轴上方有一段曲线弧Γ,其端点A、B在x轴上(但不属于Γ),对Γ上任一点P及点F1(-1,0),F2(1,0),满足: 的最大值为________.
的最大值为________.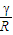 的最大值为 .
的最大值为 .