题目内容
(本题满分12分)
如图,多面体 中,底面
中,底面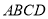 是菱形,
是菱形,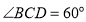 ,四边形
,四边形 是正方形,且
是正方形,且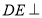 平面
平面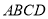 .
.

(Ⅰ)求证:  平面
平面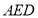 ;
;
(Ⅱ)若 ,求多面体
,求多面体 的体积
的体积 .
.
(1)见解析,(2)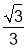
【解析】
试题分析:由于证明线面平行,直接寻找线线平行较难,所以可寻求面面平行较容易一些,从题目已知看图形可以发现,BC与AD平行,BF与DE平行,可证平面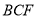
 平面
平面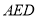 ,进而说明线面平行;第二步求多面体的体积,可转化为两个四棱锥体积之和,由于点A和点C到平面
,进而说明线面平行;第二步求多面体的体积,可转化为两个四棱锥体积之和,由于点A和点C到平面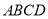 的距离相等,所以棱锥
的距离相等,所以棱锥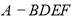 与棱锥
与棱锥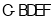 体积相等,求出
体积相等,求出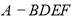 的体积乘以2即可,由于
的体积乘以2即可,由于 平面
平面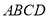 ,则
,则
平面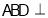 平面
平面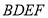 ,四边形ABCD为菱形,连接AC交BD于O,则
,四边形ABCD为菱形,连接AC交BD于O,则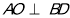 ,所以根据面面垂直的性质定理得出
,所以根据面面垂直的性质定理得出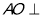 平面
平面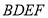 ,有了棱锥的高,再计算体积就可以了;
,有了棱锥的高,再计算体积就可以了;
试题解析:(Ⅰ)证明: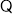
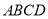 是菱形,
是菱形,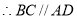 .又
.又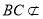 平面
平面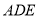 ,
,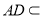 平面
平面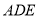 ,
,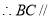 平面
平面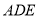 ,又
,又 平面
平面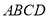 .
.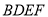 是正方形,
是正方形,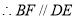 .
.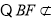 平面
平面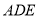 ,
,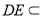 平面
平面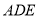 ,
, 平面
平面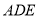 .
.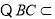 平面
平面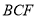 ,
,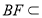 平面
平面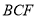 ,
, ,
, 平面
平面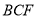
 平面
平面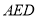 .由于
.由于 平面
平面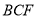 ,知
,知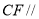 平面
平面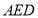 .
.
(Ⅱ)连接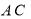 ,记
,记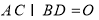 .
.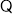
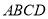 是菱形,
是菱形,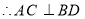 ,且
,且 .由
.由 平面
平面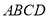 ,
,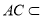 平面
平面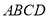 ,
,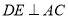 .
. 平面
平面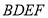 ,
,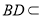 平面
平面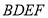 ,
,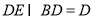 ,
,

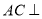 平面
平面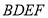 于
于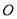 ,即
,即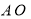 为四棱锥
为四棱锥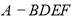 的高.
的高.
由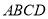 是菱形,
是菱形,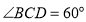 ,则
,则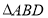 为等边三角形,由
为等边三角形,由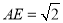 ,则
,则 ,
,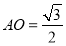 ,
,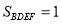 ,
,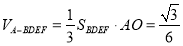 ,
,  .
.
考点:1.线面平行的证明;2.多面体的体积;

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
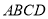 是正方形,
是正方形, 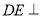 平面
平面 ,
, 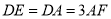 .
.
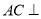
 ;
;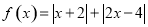 ,
,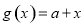 .
.
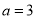 时,解不等式
时,解不等式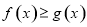 ;
;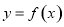 的图象,根据图象求使
的图象,根据图象求使 恒成立的实数
恒成立的实数 的取值范围.
的取值范围.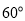 的扇形,则该几何体的侧面积为( )
的扇形,则该几何体的侧面积为( )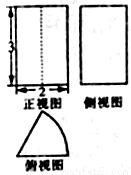
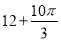
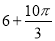
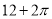
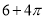
 .
.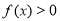 ;
;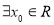 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围. 满足约束条件
满足约束条件 ,则
,则 的最小值为.
的最小值为.
 B.
B.
 D.
D.
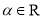 ,则“
,则“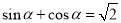 ”是“
”是“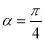 ”的( )
”的( ) 的展开式中
的展开式中 项的系数为20,则
项的系数为20,则 的最小值为 .
的最小值为 .