题目内容
12.已知过原点的动直线与圆${C_1}:{x^2}+{y^2}-6x+5=0$相交于不同的两点A,B.(1)求线段AB的中点M的轨迹C的方程;
(2)是否存在实数,使得直线L:y=k(x-4)与曲线C只有一个交点:若存在,求出的取值范围;若不存在,说明理由.
分析 (1)设当直线l的方程为y=kx,通过联立直线l与圆C1的方程,利用根的判别式大于0、韦达定理、中点坐标公式及参数方程与普通方程的相互转化,计算即得结论;
(2)通过联立直线L与圆C1的方程,利用根的判别式△=0及轨迹C的端点与点(4,0)决定的直线斜率,即得结论.
解答 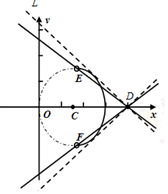 解:(1)设M(x,y),
解:(1)设M(x,y),
∵点M为弦AB中点即C1M⊥AB,
∴${k_{{C_1}M}}•{k_{AB}}=-1$即$\frac{y}{x-3}•\frac{y}{x}=-1$,
∴线段AB的中点M的轨迹的方程为${({x-\frac{3}{2}})^2}+{y^2}=\frac{9}{4}({\frac{5}{3}<x≤3})$;
(2)由(1)知点M的轨迹是以$C({\frac{3}{2},0})$为圆心$r=\frac{3}{2}$为半径的部分圆弧EF(如图所示,不包括两端点),且$E({\frac{5}{3},\frac{{2\sqrt{5}}}{3}})$,$F({\frac{5}{3},-\frac{{2\sqrt{5}}}{3}})$,又直线L:y=k(x-4)过定点D(4,0),
当直线L与圆C相切时,由$\frac{{|{k({\frac{3}{2}-4})-0}|}}{{\sqrt{{k^2}+{1^2}}}}=\frac{3}{2}$得$k=±\frac{3}{4}$,又${k_{DE}}=-{k_{DF}}=-\frac{{0-({-\frac{{2\sqrt{5}}}{3}})}}{{4-\frac{5}{3}}}=\frac{{2\sqrt{5}}}{7}$,
结合上图可知当$k∈\left\{{-\frac{3}{4},\frac{3}{4}}\right\}∪[{-\frac{{2\sqrt{5}}}{7},\frac{{2\sqrt{5}}}{7}}]$时,直线L:y=k(x-4)与曲线C只有一个交点.
点评 本题考查求轨迹方程、直线与曲线的位置关系问题,注意解题方法的积累,属于中档题.

| A. | 2$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 8$\sqrt{5}$ | D. | 20 |
| A. | y=x3 | B. | y=2x | ||
| C. | y=[x](不超过x的最大整数) | D. | y=|x| |
| A. | 3 | B. | $2\sqrt{2}$ | C. | 4 | D. | 2 |