题目内容
已知点M为△ABC所在平面上的一点，且
=
+m
，其中m为实数，若点M落在△ABC的外部，则m的取值范围是（ ）
| AM |
| 1 |
| 2 012 |
| AB |
| AC |
分析：根据平面向量基本定理，可得当m=
时，点M落在边BC上，由此可得点M落在△ABC的内部时0＜m＜
，再求以上情况的对立面，即可得到点M落在△ABC的外部，则m的取值范围．
| 2011 |
| 2012 |
| 2011 |
| 2012 |
解答：解：在AB上取一点D，使得
=
，
在AC上取一点E，使得：
=
．
则由向量的加法的平行四边形法则得：
=
+
由图可知，若点M落在△ABC的内部，则0＜m＜
．
而我们要求点M落在△ABC的外部，
因此m的取值范围是（-∞，0）∪(
，+∞)
故选C．
| AD |
| 1 |
| 2012 |
| AB |
在AC上取一点E，使得：
| AE |
| 2011 |
| 2012 |
| AC |
则由向量的加法的平行四边形法则得：
| AM |
| 1 |
| 2 012 |
| AB |
| 2011 |
| 2012 |
| AC |
由图可知，若点M落在△ABC的内部，则0＜m＜
| 2011 |
| 2012 |
而我们要求点M落在△ABC的外部，
因此m的取值范围是（-∞，0）∪(
| 2 011 |
| 2 012 |
故选C．
点评：本题给出△ABC中的向量满足的等式，求点M落在△ABC的外部时参数m的取值范围．着重考查了向量的加法法则、平面向量基本定理及其应用等知识，属于中档题．
练习册系列答案
一线名师提优试卷系列答案
相关题目
如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1，AB⊥AC，M是CC1的中点，N是BC的中点，点P在直线A1B1上，且满足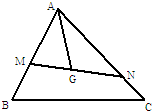
如图所示，已知点G是△ABC的重心，过G作直线与AB、AC两边分别交于M、N两点，且
＝l，
＝m，
＝n，
＝0，试求l、m、n的关系．
，则
的值为
.