题目内容

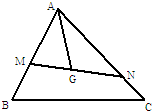精英家教网如图所示，已知点G是△ABC的重心，过G作直线与AB、AC两边分别交于M、N两点，且
AM
=x
AB
，
AN
=y
AC
，则
xy
x+y
的值为
 
．
分析：由G为三角形的重心得到
AG
=
1
3
(
AB
+
AB
)，再结合
AM
=x
AB
，
AN
=y
AC
，根据M，G，N三点共线，易得到x，y的关系式，即可得到结论．
解答：解：根据题意G为三角形的重心，
∴
AG
=
1
3
(
AB
+
AB
)，
MG
=
AG
-
AM
=
1
3
(
AB
+
AC
)-x
AB
=(
1
3
-x)
AB
+
1
3
AC
，
GN
=
AN
-
AG
=y
AC
-
AG
=y
AC
-
1
3
(
AB
+
AC
)=(y-
1
3
)
AC
-
1
3
AB
，
由于
MG
与
GN
共线，根据共线向量基本定理知，存在实数λ，使得
MG
=λ
GN
，
即(
1
3
-x)
AB
+
1
3
AC
=λ[(y-
1
3
)
AC
-
1
3
AB
]，
∴
1
3
-x=-
1
3
λ
1
3
=λ(y-
1
3
)
，
消去λ得x+y-3xy=0，
∴x+y=3xy，
即
xy
x+y
=
1
3
．
故选B．
点评：本题主要考查了三角形重心的性质，以及向量的基本定理和向量在几何中的应用，属于中档题．
练习册系列答案
相关题目
如图所示，已知圆M：（x+1）2+y2=8及定点N（1，0），点P是圆M上一动点，点Q为PN的中点，PM上一点G满足
GQ
•
NP
=0
（1）求点G的轨迹C的方程；
（2）已知直线l：y=kx+m与曲线C交于A、B两点，E（0，1），是否存在直线l，使得点N恰为△ABE的垂心？若存在，求出直线l的方程，若不存在，请说明理由．
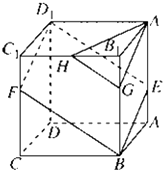精英家教网如图所示，已知ABCD-A1B1C1D1是棱长为3的正方体，点E在AA1上，点F在CC1上，G在BB1上，且AE=FC1=B1G=1，H是B1C1的中点．
（1）求证：E、B、F、D1四点共面
（2）求证：平面A1GH∥平面BED1F．
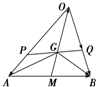精英家教网如图所示，已知点G是△ABO的重心．
（1）求
GA
+
GB
+
GO
；
（2）若PQ过△ABO的重心G，且
OA
=
a
，
OB
=
b
，
OP
=m
a
，
OQ
=n
b
，求证：
1
m
+
1
n
=3．

如图所示，已知点G是△ABC的重心，过G作直线与AB、AC两边分别交于M、N两点，且，则的值为          .

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网