题目内容
已知定点A(1,0)和定直线x=-1上的两个动点E、F,满足 ,动点P满足
,动点P满足 ,
, (其中O为坐标原点).
(其中O为坐标原点).
(1)求动点P的轨迹C的方程;
(2)过点B(0,2)的直线l与(1)中轨迹C相交于两个不同的点M、N,若 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.
解:(1)设P(x,y),E(-1,y1),F(-1,y2)(y1、y2均不为0)
由 得y1=y,即E(-1,y)
得y1=y,即E(-1,y)
由FO∥OP得 ,即F(-1,-
,即F(-1,- )
)
∵ ,∴
,∴
∴(-2,y1)•(2,y2)=0
∴y1y2=-4,∴y2=4x(x≠0)
∴动点P的轨迹C的方程为y2=4x(x≠0)
(2)设直线l的方程y=kx+2(k≠0),M( ),N(
),N( )
)
联立得 消去x得ky2-4y+8=0
消去x得ky2-4y+8=0
∴ ,
, ,且△=16-32k>0即k<
,且△=16-32k>0即k< .
.
∴ =(
=( )•(
)•( )=(
)=( )•(
)•( )+y1y2
)+y1y2
= =
=
∵ ,∴-12<k<0,满足k<
,∴-12<k<0,满足k< ,
,
∴-12<k<0.
分析:(1)用坐标表示出 的坐标,利用
的坐标,利用 即得动点P的轨迹方程;
即得动点P的轨迹方程;
(2)设出直线的方程与抛物线方程联立,利用韦达定理及 ,利用数量积公式,即可求得直线l的斜率的取值范围.
,利用数量积公式,即可求得直线l的斜率的取值范围.
点评:本题考查轨迹方程,考查直线与抛物线的位置关系,考查向量知识的运用,考查韦达定理,考查学生的计算能力,属于中档题.
由
 得y1=y,即E(-1,y)
得y1=y,即E(-1,y)由FO∥OP得
 ,即F(-1,-
,即F(-1,- )
)∵
 ,∴
,∴
∴(-2,y1)•(2,y2)=0
∴y1y2=-4,∴y2=4x(x≠0)
∴动点P的轨迹C的方程为y2=4x(x≠0)
(2)设直线l的方程y=kx+2(k≠0),M(
 ),N(
),N( )
)联立得
 消去x得ky2-4y+8=0
消去x得ky2-4y+8=0∴
 ,
, ,且△=16-32k>0即k<
,且△=16-32k>0即k< .
.∴
 =(
=( )•(
)•( )=(
)=( )•(
)•( )+y1y2
)+y1y2=
 =
=
∵
 ,∴-12<k<0,满足k<
,∴-12<k<0,满足k< ,
,∴-12<k<0.
分析:(1)用坐标表示出
 的坐标,利用
的坐标,利用 即得动点P的轨迹方程;
即得动点P的轨迹方程;(2)设出直线的方程与抛物线方程联立,利用韦达定理及
 ,利用数量积公式,即可求得直线l的斜率的取值范围.
,利用数量积公式,即可求得直线l的斜率的取值范围.点评:本题考查轨迹方程,考查直线与抛物线的位置关系,考查向量知识的运用,考查韦达定理,考查学生的计算能力,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
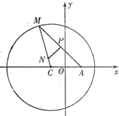 如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足
如图,已知定点A(1,0),定圆C:(x+1)2+y2=8,M为圆C上的一个动点,点P在线段AM上,点N在线段CM上,且满足