题目内容
14.已知函数f(x)是R上的奇函数,g(x)是R上的偶函数,且有g(1)=0,当x>0时,有f′(x)g(x)+f(x)g′(x)>0,则f(x)g(x)>0的解集为(-1,0)∪(1,+∞).分析 先根据f′(x)g(x)+f(x)g′(x)>0可确定[f(x)g(x)]'>0,进而可得到f(x)g(x)在x>0时递增,结合函数f(x)与g(x)的奇偶性可确定f(x)g(x)在x<0时也是增函数,最后根据g(1)=0可求得答案.
解答 解:因 f′(x)g(x)+f(x)g′(x)>0,即[f(x)g(x)]'>0,
f(x)g(x)在x>0时递增,
又∵f(x),g(x)分别是定义R上的奇函数和偶函数,
∴f(x)g(x)为奇函数,关于原点对称,
∴f(x)g(x)在x<0时也是增函数.
∵f(1)g(1)=0,
∴f(-1)g(-1)=0
∴f(x)g(x)>0的解集为:x>1或-1<x<0
故答案为:(-1,0)∪(1,+∞)
点评 本题考查了函数的奇偶性的应用,以及导数的运算,不等式的解法等,根据导数的正负可以确定函数的单调性,利用数形结合的思想进行解题.属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
9.已知函数f(x)满足f(x)=f(π-x),且当x∈(-$\frac{π}{2}$,$\frac{π}{2}$)时,f(x)=ex+sinx,则( )
| A. | $f(\frac{π}{3})<f(\frac{π}{4})<f(\frac{5π}{6})$ | B. | $f(\frac{π}{4})<f(\frac{π}{3})<f(\frac{5π}{6})$ | C. | $f(\frac{π}{4})<f(\frac{5π}{6})<f(\frac{π}{3})$ | D. | $f(\frac{5π}{6})<f(\frac{π}{4})<f(\frac{π}{3})$ |
19.为了调查胃病是否与生活规律有关,在某地对540名40岁以上的人进行了调查,结果是:患胃病者生活不规律的共80人,患胃病者生活规律的共20人,未患胃病者生活不规律的共240人,未患胃病者生活规律的共200人.
(1)根据以上数据列出2×2列联表.
(2)能否在犯错误的概率不超过0.001的前提下认为40岁以上的人患胃病和生活规律有关系?
参考公式与临界值表:${K_{\;}}^2=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(1)根据以上数据列出2×2列联表.
(2)能否在犯错误的概率不超过0.001的前提下认为40岁以上的人患胃病和生活规律有关系?
参考公式与临界值表:${K_{\;}}^2=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| ko | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
4.已知椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1的左、右焦点分别为F1,F2,P为椭圆上不同于长轴端点的任意一点,则△PF1F2内切圆半径的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
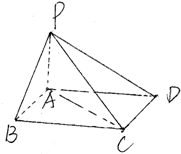 如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,PA=AB=1,BC=2,PA⊥底面ABCD
如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,PA=AB=1,BC=2,PA⊥底面ABCD