题目内容
9.己知函数f(x)=2x+1,数列{an}的前n项和Sn=f(n2)-1,数列{bn}满足bn=f(bn-1),且b1=1.(1)分别求{an},{bn}的通项公式;
(2)记cn=$\frac{{a}_{n}}{2{(b}_{n}+1)}$,求数列{cn}的前n项和.
分析 (1)分类讨论求数列{an}的通项公式,由构造法可得{bn+1}是以2为首项,2为公比的等比数列,从而求得;
(2)化简cn=$\frac{{a}_{n}}{2{(b}_{n}+1)}$=$\frac{4n-2}{{2}^{n+1}}$,从而利用错位相减法求数列的前n项和即可.
解答 解:(1)由题意知,Sn=f(n2)-1=2n2+1-1=2n2,
当n=1时,a1=S1=2,
当n≥2时,an=Sn-Sn-1=4n-2,
当n=1时也成立,
故an=4n-2;
∵bn=f(bn-1)=2bn-1+1,
∴bn+1=2(bn-1+1),
故{bn+1}是以2为首项,2为公比的等比数列,
故bn+1=2n,
故bn=2n-1.
(2)cn=$\frac{{a}_{n}}{2{(b}_{n}+1)}$=$\frac{4n-2}{{2}^{n+1}}$,设{cn}的前n项和Tn,
故Tn=$\frac{2}{4}$+$\frac{6}{8}$+…+$\frac{4n-2}{{2}^{n+1}}$,
2Tn=$\frac{2}{2}$+$\frac{6}{4}$+$\frac{10}{8}$+…+$\frac{4n-2}{{2}^{n}}$,
故Tn=1+$\frac{4}{4}$+$\frac{4}{8}$+…+$\frac{4}{{2}^{n}}$-$\frac{4n-2}{{2}^{n+1}}$=3-$\frac{2}{{2}^{n-1}}$-$\frac{4n-2}{{2}^{n+1}}$.
点评 本题考查了数列的性质的判断与应用,同时考查了分类讨论的思想及整体思想的应用,同时考查了构造法与错位相减法的应用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
14.函数y=$\left\{\begin{array}{l}{2x,x≥0}\\{-{x}^{2},x<0}\\{\;}\end{array}\right.$的反函数是( )
| A. | y=$\left\{\begin{array}{l}{\frac{x}{2},x≥0}\\{\sqrt{-x},x<0}\\{\;}\end{array}\right.$ | B. | y=$\left\{\begin{array}{l}{\frac{x}{2},x≥0}\\{-\sqrt{-x},x<0}\\{\;}\end{array}\right.$ | ||
| C. | y=$\left\{\begin{array}{l}{2x,x≥0}\\{\sqrt{-x},x<0}\end{array}\right.$ | D. | y=$\left\{\begin{array}{l}{2x,x≥0}\\{-\sqrt{-x},x<0}\\{\;}\end{array}\right.$ |
1.已知集合A={x|x≥1},$B=\{x|\frac{x-2}{x}≤0\}$,则A∩(∁RB)=( )
| A. | (2,+∞) | B. | [1,2] | C. | (0,+∞) | D. | (-∞,0]∪[1,+∞) |
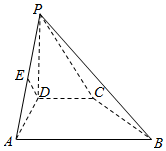 如图,在四棱锥P-ABCD中,PD⊥面ABCD,AB∥DC,AB⊥AD,DC=6,AD=8,BC=10,∠PAD=45°,E为PA的中点.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AB∥DC,AB⊥AD,DC=6,AD=8,BC=10,∠PAD=45°,E为PA的中点.