题目内容
求证:![]() =tanα.
=tanα.
证明:左边=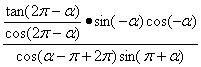
=![]()
=![]()
=tanα=右边,
∴原等式成立.
点评:由于诱导公式二、三中的α可以是任意角,为了运用公式二、三,可以把-α、α-π等作为一个整体,看成公式中的“α”,对于正切和余切可以切化弦后再用诱导公式.

练习册系列答案
相关题目
题目内容
求证:![]() =tanα.
=tanα.
证明:左边=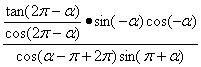
=![]()
=![]()
=tanα=右边,
∴原等式成立.
点评:由于诱导公式二、三中的α可以是任意角,为了运用公式二、三,可以把-α、α-π等作为一个整体,看成公式中的“α”,对于正切和余切可以切化弦后再用诱导公式.
