题目内容
AB是半圆的直径,P为半圆周上一点,SA垂直于半圆所在平面.(1)设A在SB、SP上的射影分别为H、N,求证:AN⊥平面SPB;
(2)证明∠AHN是二面角ASBP的平面角;
(3)若∠ASB=60°,∠PAB=α,∠AHN=β,求证:tanαtanβ=2.

证明:
(1)AB是直径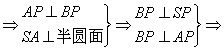 BP⊥平面SAP
BP⊥平面SAP![]()
![]()
![]() AN⊥平面SPB.
AN⊥平面SPB.
(2)由(1)AN⊥平面SPB![]()
![]()
![]() SB⊥平面AHN
SB⊥平面AHN![]() ∠AHN是二面角ASBP的平面角.
∠AHN是二面角ASBP的平面角.
(3)∠SAB=60°![]() SB=2SA
SB=2SA

![]() tanα·tanβ=
tanα·tanβ=![]() =2.
=2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.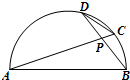 (2012•深圳二模)(几何证明选讲选做题)如图,AB是半圆的直径,弦AC和弦BD相交于点P,且AB=3DC,则sin∠APD=
(2012•深圳二模)(几何证明选讲选做题)如图,AB是半圆的直径,弦AC和弦BD相交于点P,且AB=3DC,则sin∠APD= 的属于特征值b的一个特征向量为
的属于特征值b的一个特征向量为 ,求实数a、b的值.
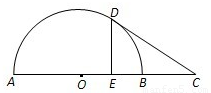
,求实数a、b的值. (t为参数,p为正常数),求p的值.
(t为参数,p为正常数),求p的值.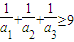 .
.
 A.(本小题为选做题,满分10分)
A.(本小题为选做题,满分10分) ,其中
,其中 ,若点P(1,1)在矩阵A的变换下得到点
,若点P(1,1)在矩阵A的变换下得到点 ,
, 分别是曲线
分别是曲线 和
和 上的动点,求动点
上的动点,求动点 为正数,证明:
为正数,证明: ≥
≥ .
.