题目内容
在等差数列{an}中,已知a1+a2=4,a2+a3=8,则a7等于( )
| A、7 | B、10 | C、13 | D、19 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:根据题意和等差数列的通项公式列出方程,求出a1和d的值,再求出a7.
解答:
解:设等差数列{an}的公差是d,
因为a1+a2=4,a2+a3=8,
所以
,解得
,
所以a7=a1+6d=1+12=13,
故选:C.
因为a1+a2=4,a2+a3=8,
所以
|
|
所以a7=a1+6d=1+12=13,
故选:C.
点评:本题考查等差数列的通项公式的应用,属于基础题.

练习册系列答案
相关题目
已知向量
=(1,k),
=(k-1,2),若
∥
,则正实数k的值为( )
| a |
| b |
| a |
| b |
| A、2 | B、1 |
| C、1或-2 | D、-1或2 |
已知a,b是实数,则“a>2且b>2”是“a+b>4且ab>4”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
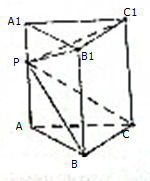 如图所示,点P为三棱柱ABC-A1B1C1侧棱AA1上一动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为( )
如图所示,点P为三棱柱ABC-A1B1C1侧棱AA1上一动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为( )| A、2V | ||
| B、3V | ||
C、
| ||
D、
|
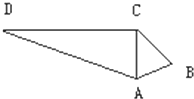 如图在四边形ABCD中,AC⊥DC,△ADC的面积为30cm2,DC=12cm,AB=3cm,BC=4cm求△ABC的面积.
如图在四边形ABCD中,AC⊥DC,△ADC的面积为30cm2,DC=12cm,AB=3cm,BC=4cm求△ABC的面积.