题目内容
函数f(x)=xe-x,x∈[0,4]的最大值是( )
| A、0 | ||
B、
| ||
C、
| ||
D、
|
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:利用导数判断函数的单调性即可得出结论.
解答:
解:f(x)=e-x-xe-x=e-x(1-x),
∴当0≤x≤1时,f′(x)≥0,f(x)单调递增,
当1≤x≤4时,f′(x)≤0,f(x)单调递减,
∴当x=1时,f(x)max=f(1)=
.
故选B.
∴当0≤x≤1时,f′(x)≥0,f(x)单调递增,
当1≤x≤4时,f′(x)≤0,f(x)单调递减,
∴当x=1时,f(x)max=f(1)=
| 1 |
| e |
故选B.
点评:本题主要考查利用导数求函数的最值知识,属基础题.

练习册系列答案
相关题目
已知点A(1,1),B(4,2)和向量
=(2,λ),若
∥
,则实数λ的值为( )
| a |
| a |
| AB |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
已知袋中有3个红球2个白球,从中任取一个,恰为红球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题,正确的是( )
| A、a,b,c∈R,且a>b,则ac>bc | ||||
B、a,b∈R,且ab≠0,则
| ||||
| C、复数Z=i-1对应的点在第四象限 | ||||
| D、a,b∈R,且|a|>|b|,则a2>b2 |
从混有5张假钞的20张百元钞票中任意抽取两张2张,将其中一张在验钞机上检验发现是假钞,问这2张都是假钞的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知△ABC中,角A、B、C所对的边分别是a、b、c;且a=1,b=2,C=150°,则△ABC的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
已知等差数列{an}中,a3+a8=22,a6=7,则a5的值为( )
| A、5 | B、15 | C、20 | D、25 |
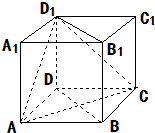 如图,在正方体ABCD-A1B1C1D1中.求证:平面ACD1⊥平面BB1D1D.
如图,在正方体ABCD-A1B1C1D1中.求证:平面ACD1⊥平面BB1D1D.