Question

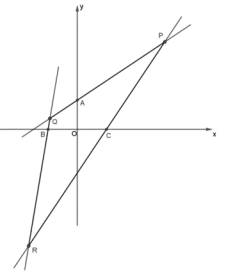
【题目】函数y = f(x)是定义域为R的偶函数，当x≥0时，函数f(x)的图象是由一段抛物线和一条射线组成（如图所示）．

①当时，y的取值范围是______；

②如果对任意 (b <0)，都有，那么b的最大值是______．

Answer 1

【答案】

【解析】

①根据f（x）是偶函数，图象关于y轴对称，结合图象可得y的取值范围．

②当x≥0时，设抛物线的方程为y=ax2+bx+c，求解解析式，根据f（x）是定义域为R的偶函数，可得x＜0的解析式，令y=1，可得x对应的值，结合图象可得b的最大值．

由图象可知，当时，函数在上的最小值，

当时，函数在上的最小值，

所以当，函数的值域为；

当时，函数，当时，函数，

当时，或，

又因为函数为偶函数，图象关于轴对称，

所以对于任意，要使得，则，或，

则实数的最大值是．

故答案为：