题目内容
7. 某高校为调查1000名学生每周的自习时间(单位:小时),从中随机抽查了100名学生每周的自习时间,制成了如图所示的频率分布直方图,其中自习时间范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是700.
某高校为调查1000名学生每周的自习时间(单位:小时),从中随机抽查了100名学生每周的自习时间,制成了如图所示的频率分布直方图,其中自习时间范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,这200名学生中每周的自习时间不少于22.5小时的人数是700.
分析 由频率分布直方图求出每周自习时间不少于22.5小时的频率,由此能求出每周自习时间不少于22.5小时的人数.
解答 解:由频率分布直方图可知每周自习时间不少于22.5小时的频率为:
(0.16+0.08+0.04)×2.5=0.7,
∴每周自习时间不少于22.5小时的人数为0.7×1000=700.
故答案为:700.
点评 本题考查频数的求法,考查频率分布直方图等基础知识,考查数据处理能力、运算求解能力,考查数形结合思想,是基础题.

练习册系列答案
相关题目
1.已知函数f(x)=$\left\{{\begin{array}{l}{-{x^2}+2x}&{x∈({-∞,2})}\\{3f({x-2})}&{x∈[{2,+∞})}\end{array}}$,则函数g(x)=f(x)-cosπx在区间[0,6]内所有零点的和为( )
| A. | 18 | B. | 20 | C. | 36 | D. | 40 |
15.甲、乙两人参加歌唱比赛,晋级概率分别为$\frac{4}{5}$和$\frac{3}{4}$,且两人是否晋级相互独立,则两人中恰有一人晋级的概率为( )
| A. | $\frac{19}{20}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{7}{20}$ |
2. 为了解某市居民用水情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将数据分成[0,0.5),[0.5,1),…,[4,4.5)9组,绘制成了如图所示的频率分布直方图.由图可知,居民月均用水量的众数、中位数的估计值分别为( )
为了解某市居民用水情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将数据分成[0,0.5),[0.5,1),…,[4,4.5)9组,绘制成了如图所示的频率分布直方图.由图可知,居民月均用水量的众数、中位数的估计值分别为( )
 为了解某市居民用水情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将数据分成[0,0.5),[0.5,1),…,[4,4.5)9组,绘制成了如图所示的频率分布直方图.由图可知,居民月均用水量的众数、中位数的估计值分别为( )
为了解某市居民用水情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将数据分成[0,0.5),[0.5,1),…,[4,4.5)9组,绘制成了如图所示的频率分布直方图.由图可知,居民月均用水量的众数、中位数的估计值分别为( )| A. | 2.25,2.25 | B. | 2.25,2.02 | C. | 2,2.5 | D. | 2.5,2.25 |
14.执行图示的程序框图,则输出的结果为( )
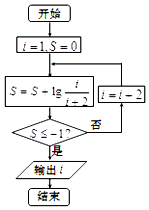

| A. | 7 | B. | 9 | C. | 10 | D. | 11 |
18.设命题p:?x∈R,x02>lnx,则¬p为( )
| A. | ?x0∈R,x02>lnx0 | B. | ?x0∈R,x02≥lnx0 | C. | ?x0∈R,x02<lnx0 | D. | ?x0∈R,x02≤lnx0 |