题目内容
【题目】如图,在△ABC中,∠BAC=120°,AC=3,△ABC的面积等于 ![]() ,D为边长BC上一点.
,D为边长BC上一点. 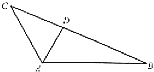
(1)求BC的长;
(2)当AD= ![]() 时,求cos∠CAD的值.
时,求cos∠CAD的值.
【答案】
(1)解:在△ABC中,∠BAC=120°,AC=3,△ABC的面积等于 ![]() ACABsin∠BAC=
ACABsin∠BAC= ![]() 3AB
3AB ![]() =
= ![]() ,
,
∴AB=5,再由余弦定理可得BC2=AB2+AC2﹣2ABACcos∠BAC=25+9﹣2×5×3×(﹣ ![]() )=49,
)=49,
∴BC=7.
(2)解:由题意可得cosC= ![]() =
= ![]() ,sinC=
,sinC= ![]() .
.
D为边长BC上一点,当AD= ![]() 时,△ACD中,利用正弦定理可得
时,△ACD中,利用正弦定理可得 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
求得sin∠ADC= ![]() ,∴cos∠ADC=±
,∴cos∠ADC=± ![]() =±
=± ![]() .
.
当 cos∠ADC= ![]() ,cos∠CAD=﹣cos(C+∠ADC)=﹣cosCcos∠ADC+sinCsin∠ADC
,cos∠CAD=﹣cos(C+∠ADC)=﹣cosCcos∠ADC+sinCsin∠ADC
=﹣ ![]()
![]() +
+ ![]()
![]() =
= ![]() .
.
当 cos∠ADC=﹣ ![]() ,cos∠CAD=﹣cos(C+∠ADC)=﹣cosCcos∠ADC+sinCsin∠ADC
,cos∠CAD=﹣cos(C+∠ADC)=﹣cosCcos∠ADC+sinCsin∠ADC
=﹣ ![]() (﹣
(﹣ ![]() )+
)+ ![]()
![]() =
= ![]()
【解析】(1)由条件利用余弦定理、三角形的面积公式先求得AB的值,可得BC的值.(2)利用正弦定理求得sin∠ADC 的值,可得cos∠ADC 的值,再利用两角和的余弦公式,求得cos∠CAD=﹣cos(C+∠ADC)的值.
【考点精析】本题主要考查了余弦定理的定义的相关知识点,需要掌握余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目