题目内容
定义: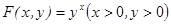 ,已知数列
,已知数列 满足
满足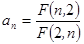
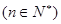 ,若对任意正整数
,若对任意正整数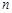 ,都有
,都有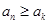
 成立,则
成立,则 的值为 ( )
的值为 ( )
| A.2 | B.1 | C.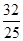 | D.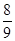 |
D
解析试题分析:根据新定义,: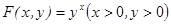 ,那么可知,
,那么可知, ,因为对于任意正整数
,因为对于任意正整数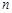 ,都有
,都有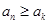
 成立,则可知
成立,则可知 ,当n=1,不等式成立,可知
,当n=1,不等式成立,可知 ,当n=2时,
,当n=2时, ,当n=3时,
,当n=3时, ,,n=4时,则
,,n=4时,则 ,依次以后
,依次以后 将增大,可知结论为
将增大,可知结论为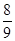 ,选D.
,选D.
那么可知 的值为
的值为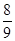 ,故选D.
,故选D.
考点:考查了数列的新定义。
点评:解决该试题的关键是对于数列定义的理解和不等式恒成立的转换,属于中档题。

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
不等式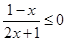 的解集为( )
的解集为( )
A.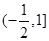 | B. |
C.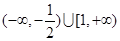 | D.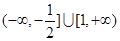 |
二次不等式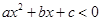 的解集是全体实数的条件是( )
的解集是全体实数的条件是( )
A.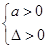 | B. | C.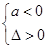 | D.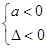 |
已知x>0,y>0,x+y+xy="2," 则x+y的最小值是
A.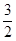 | B.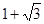 | C. | D. |
方程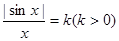 有且仅有两个不同的实数解
有且仅有两个不同的实数解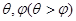 ,则以下结论正确的为( )
,则以下结论正确的为( )
A.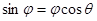 | B. |
C.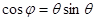 | D. |
若不等式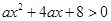 的解集为
的解集为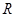 ,则实数
,则实数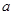 的取值范围是
的取值范围是
A.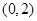 | B.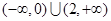 |
C.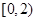 | D.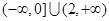 |
关于 的不等式
的不等式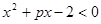 的解集是
的解集是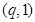 ,则
,则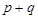 的值为( )
的值为( )
A. | B.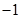 | C.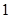 | D.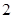 |
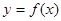 的图象是中心在原点,焦点在
的图象是中心在原点,焦点在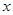 轴上的椭圆的两段弧,则不等式
轴上的椭圆的两段弧,则不等式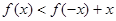 的解集为 ( )
的解集为 ( )



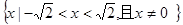
 的解集为( )
的解集为( )






