题目内容
方程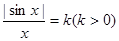 有且仅有两个不同的实数解
有且仅有两个不同的实数解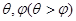 ,则以下结论正确的为( )
,则以下结论正确的为( )
A.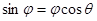 | B. |
C.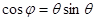 | D. |
B
解析试题分析:依题意可知x>0(x不能等于0)
令 ,
, ,然后分别做出两个函数的图象.
,然后分别做出两个函数的图象.
因为原方程有且只有两个解,所以y2与y1仅有两个交点,而且第二个交点是y1和y2相切的点,
即点 为切点,因为
为切点,因为 ,所以切线的斜率
,所以切线的斜率 .而且点
.而且点 在切线
在切线 上.
上.
于是将点 代入切线方程
代入切线方程 可得:
可得: .故选B.
.故选B.
考点:正弦函数的图象.
点评:本题考查数形结合的思想,函数图象的交点,就是方程的根,注意:y1的图象只有X轴右半部分和y轴上半部分,且原点处没有值(因为x不等于0);y2的图象是过原点的一条直线.

练习册系列答案
相关题目
不等式 的解集是
的解集是 ,则a+b的值是( )
,则a+b的值是( )
| A.-3 | B.-1 | C.1 | D.3 |
不等式 >0的解集是
>0的解集是
| A.(2,+∞) | B.(-2,1)∪(2,+∞) |
| C.(-2,1) | D.(-∞,-2)∪(1,+∞) |
若关于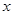 的不等式
的不等式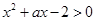 在区间
在区间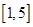 上有解,则实数
上有解,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C.(1,+∞) | D.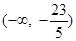 |
若不等式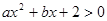 的解为
的解为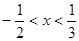 ,则
,则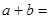 ( )
( )
| A.14 | B.-14 | C.-2 | D.12 |
定义: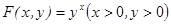 ,已知数列
,已知数列 满足
满足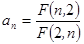
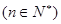 ,若对任意正整数
,若对任意正整数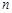 ,都有
,都有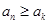
 成立,则
成立,则 的值为 ( )
的值为 ( )
| A.2 | B.1 | C.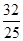 | D.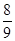 |
若不等式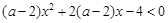 对一切
对一切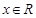 恒成立,则实数
恒成立,则实数 取值的集合( )
取值的集合( )
A.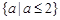 | B.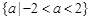 |
C.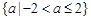 | D.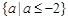 |
不等式 的解集为 ( )
的解集为 ( )
A. | B. |
C.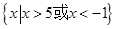 | D.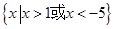 |
设函数 则满足
则满足 的x的取值范围是
的x的取值范围是
A. | B. | C. | D. |