题目内容
若不等式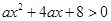 的解集为
的解集为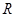 ,则实数
,则实数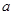 的取值范围是
的取值范围是
A.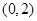 | B.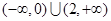 |
C.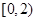 | D.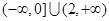 |
C
解析试题分析:当 时显然成立;当
时显然成立;当 ,需
,需 。综上所述:
。综上所述: 。选C。
。选C。
考点:本题主要考查一元二次不等式的恒成立问题。
点评:当二次项系数含参数时,要首先讨论其是否为0.本题易错,忽视讨论。

练习册系列答案
相关题目
函数 的最小值为( )
的最小值为( )
A. | B.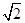 | C.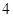 | D. |
若关于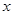 的不等式
的不等式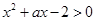 在区间
在区间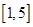 上有解,则实数
上有解,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C.(1,+∞) | D.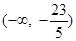 |
定义: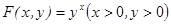 ,已知数列
,已知数列 满足
满足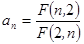
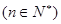 ,若对任意正整数
,若对任意正整数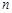 ,都有
,都有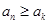
 成立,则
成立,则 的值为 ( )
的值为 ( )
| A.2 | B.1 | C.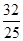 | D.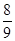 |
若不等式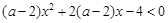 对一切
对一切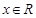 恒成立,则实数
恒成立,则实数 取值的集合( )
取值的集合( )
A.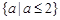 | B.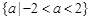 |
C.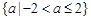 | D.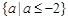 |
设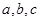 均为正数,且
均为正数,且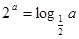 ,
,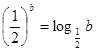 ,
,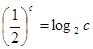 则( )
则( )
A. | B.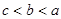 | C.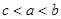 | D.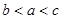 |
不等式 的解集为 ( )
的解集为 ( )
A. | B. |
C.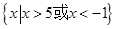 | D.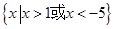 |
不等式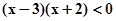 的解集为( )
的解集为( )
A.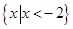 | B. | C.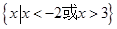 | D.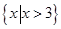 |
不等式 的解集是( )
的解集是( )
A. | B. |
C. | D. |