Question

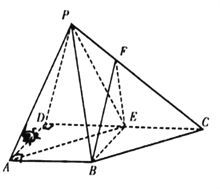
【题目】如图，矩形所在的平面与正方形所在的平面相互垂直，是的中点．

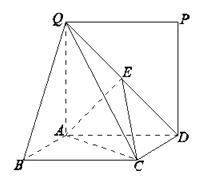
（Ⅰ）求证：∥平面；

（Ⅱ）求证：平面⊥平面；

（Ⅲ）若，，求多面体的体积．

Answer 1

【答案】（Ⅰ）详见解析（Ⅱ）详见解析（Ⅲ）1

【解析】

试题（Ⅰ）连接BD交AC于O，连接EO．证明EO∥QB，即可证明QB∥平面AEC；（Ⅱ）证明CD⊥AE，AE⊥QD．推出AE⊥平面QDC，然后证明平面QDC⊥平面AEC；（Ⅲ）通过多面体ABCEQ为四棱锥Q-ABCD截去三棱锥E-ACD所得，计算求解即可

试题解析：（Ⅰ）证明：连接交于，连接．

因为 分别为和的中点，则∥．

又 平面，平面，

所以 ∥平面

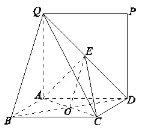
（Ⅱ）证明： 因为矩形所在的平面与正方形所在的平面相互垂直，

平面，，

所以平面．

又平面， 所以．

因为，是的中点， 所以．

所以平面．

所以平面⊥平面．

（Ⅲ）解：多面体为四棱锥截去三棱锥所得，

所以．