题目内容
【题目】已知椭圆
的中心在原点
，直线
与坐标轴的交点是椭圆的两个顶点.
（1）求椭圆的方程；
（2）若
是椭圆上的两点，且满足
，求
的最小值.
【答案】（1）
； （2）
.
【解析】
（1）因为
与
轴交点为
，与
轴交点为
，
又直线
与坐标轴交点为椭圆
的顶点，即可求得a,b,进而得到椭圆的方程；
（2）由题意知M、N是椭圆上的两点，且OM⊥ON，故设M（r1cosθ，r1sinθ），N（-r2sinθ，r2cosθ），由题设条件能够推出|MN|的最小值为．
（1）因为与轴交点为，与轴交点为，
又直线与坐标轴交点为椭圆的顶点，
所以椭圆的顶点为，，
故所求椭圆方程为
（2）由题意知
是椭圆上的两点，且
，故设
，
，其中
，
，
于是
，
，
从而
.
又
（当且仅当
时取等号）
所以
，即
，
.
故所求
的最小值为.
练习册系列答案
计算高手系列答案
相关题目
【题目】甲、乙两人在相同条件下各射击
次，每次中靶环数情况如图所示：
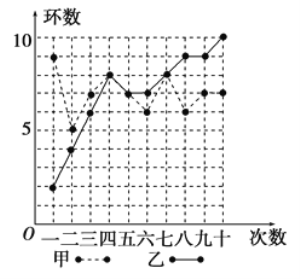
（1）请填写下表（先写出计算过程再填表）：
平均数 | 方差 | 命中 | |
甲 |
|
|
|
乙 |
（2）从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看（分析谁的成绩更稳定）；
②从平均数和命中
环及环以上的次数相结合看（分析谁的成绩好些）；
③从折线图上两人射击命中环数的走势看（分析谁更有潜力）.
