题目内容
连接抛物线 的焦点
的焦点 与点
与点 所得的线段与抛物线交于点
所得的线段与抛物线交于点 ,设点
,设点 为坐标原点,则三角形
为坐标原点,则三角形 的面积为( )
的面积为( )
A. | B. | C. | D. |
B
解析试题分析:因为F(0,1),所以直线FM的方程为x+y-1=0,与抛物线联立 消x得
消x得
 .
.
考点:直线与抛物线的位置关系,三角形的面积公式.
点评:本小题在知识三角形OAM底边OM的情况下,求点A的纵坐标是解本小题的关键,因而直线FM的方程与抛物线的方程联立,消去x解关于y的一元二次方程即可解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B. | C.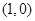 | D. |
设 、
、 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线 上一点,
上一点, 是底角为
是底角为 的等腰三角形,则
的等腰三角形,则 的离心率为( )
的离心率为( )
A. | B. | C.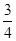 | D. |
 上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( )
上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是( )
 是抛物线
是抛物线 的焦点,
的焦点, 是该抛物线上的动点,则线段
是该抛物线上的动点,则线段 中点的轨迹方程是( )
中点的轨迹方程是( )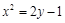



 的左焦点
的左焦点 作圆
作圆 的切线,切点为
的切线,切点为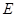 ,延长
,延长 交抛物线
交抛物线 于点
于点 ,若
,若 的中点,则双曲线的离心率为( )
的中点,则双曲线的离心率为( )

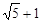

 ,过右焦点F作不垂直于
,过右焦点F作不垂直于 轴的弦交椭圆于A、B两点,AB的垂直平分线交
轴的弦交椭圆于A、B两点,AB的垂直平分线交 B.
B. C.
C. D.
D.
 ,直线
,直线 的方程为
的方程为 ,在抛物线上有一动点P到y轴的距离为
,在抛物线上有一动点P到y轴的距离为 ,P到直线
,P到直线 ,则
,则 的最小( )
的最小( )
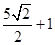


 的左、右顶点分别为A、B,点P是第一象限内双曲线上的点.若直线PA、PB的倾斜角分别为α,β,且
的左、右顶点分别为A、B,点P是第一象限内双曲线上的点.若直线PA、PB的倾斜角分别为α,β,且 ,那么α的值是( )
,那么α的值是( ) B.
B.
 D.
D.