��Ŀ����
8����������ʽ��$\left\{\begin{array}{l}{x-y+5��0}\\{x+y��0}\\{x��3}\end{array}\right.$��ʾ��ƽ���������ƽ������ΪA���ڴ������½���������⣺��1����A�������
��2����B={��x-y��x+y��|��x��y����A}����B�������
��3����z=3x+y����ֵ��
��4����z=x2+��y+1��2����Сֵ��
��5����z=$\frac{y+1}{x+1}$��ֵ��
��6����z=ax+y��a��1�������ֵ��
���� ��1����������ʽ���Ӧ��ƽ����������������꣬������A�������
��2����m=x-y��n=x+y��ת��Ϊ����m��n�IJ���ʽ�鼴����B�������
��3������ֱ�ߵĽؾ࣬������z=3x+y����ֵ��
��4�����ݵ㵽ֱ�ߵľ��빫ʽ������z=x2+��y+1��2����Сֵ��
��5������������б�ʹ�ϵ������z=$\frac{y+1}{x+1}$��ֵ��
��6������ֱ�ߵĽؾ��z�Ĺ�ϵ������z=ax+y��a��1�������ֵ��
��� 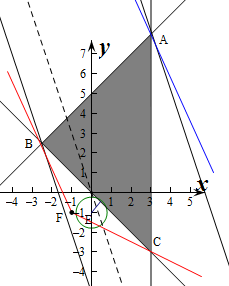 �⣺��1����������ʽ���Ӧ��ƽ��������ͼ��
�⣺��1����������ʽ���Ӧ��ƽ��������ͼ��
��$\left\{\begin{array}{l}{x-y+5}\\{x=3}\end{array}\right.$��$\left\{\begin{array}{l}{x=3}\\{y=8}\end{array}\right.$����A��3��8����
��$\left\{\begin{array}{l}{x=3}\\{x+y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=3}\\{y=-3}\end{array}\right.$����C��3��-3����
��$\left\{\begin{array}{l}{x-y+5=0}\\{x+y=0}\end{array}\right.$��$\left\{\begin{array}{l}{x=-\frac{5}{2}}\\{y=\frac{5}{2}}\end{array}\right.$����B��-$\frac{5}{2}$��$\frac{5}{2}$����
��|AC|=8-��-3��=11��B��ֱ��x=3�ľ���d=3-��-$\frac{5}{2}$��=$\frac{11}{2}$��
��A�����S=$\frac{1}{2}��11��\frac{11}{2}=\frac{121}{4}$��
��2����B={��x-y��x+y��|��x��y����A}����B�������
��m=x-y��n=x+y��
��x=$\frac{m+n}{2}$��y=$\frac{n-m}{2}$��
���ز���ʽ��$\left\{\begin{array}{l}{x-y+5��0}\\{x+y��0}\\{x��3}\end{array}\right.$��$\left\{\begin{array}{l}{m+5��0}\\{n��0}\\{\frac{m+n}{2}��3}\end{array}\right.$��
��$\left\{\begin{array}{l}{m��-5}\\{n��0}\\{m+n��6}\end{array}\right.$����Ӧ��ƽ������Ϊ��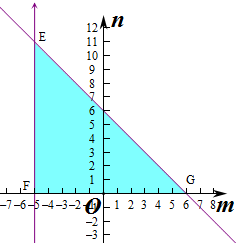
����G��6��0����F��-5��0����E��-5��11����
��GF=6-��-5��=11��EF=11��
��������EFG�����S=$\frac{1}{2}��11��11$=$\frac{121}{2}$��
��3����z=3x+y����y=-3x+z��
ƽ��ֱ��y=-3x+z�����ߣ�����ͼ���֪��ֱ��y=-3x+z��������Aʱ��ֱ��y=-3x+z�Ľؾ����
��ʱz���Ϊz=3��3+8=9+8=17��
ƽ��ֱ��y=-3x+z����ͼ���֪��ֱ��y=-3x+z��������Bʱ��ֱ��y=-3x+z�Ľؾ���С��
��ʱz��СΪz=3����-$\frac{5}{2}$��+$\frac{5}{2}$=-5��
��4��z=x2+��y+1��2�ļ�������Ϊ�����ڵĵ㵽����E��0��-1���ľ��룬
��ͼ��֪E��BC�ľ�����С����ʱ����d=$\frac{|1|}{\sqrt{2}}=\frac{1}{\sqrt{2}}$��
��z����СֵΪz=d2=$\frac{1}{2}$��
��5��z=$\frac{y+1}{x+1}$�ļ�������Ϊ�����ڵĵ㵽��F��-1��-1����б�ʣ����ߣ���
BF���k=$\frac{\frac{5}{2}+1}{-\frac{5}{2}+1}$=-2��CF���k=$\frac{-3+1}{3+1}=-\frac{1}{2}$��
��z$��-\frac{1}{2}$��z��-2��
��z��ֵ��Ϊ{z|z$��-\frac{1}{2}$��z��-2}��
��6����z=ax+y��a��1����y=-ax+z�����k=-a��-1��
ƽ��ֱ��y=-ax+z����ͼ��֪��ֱ��y=-ax+z������Aʱֱ�ߵĽؾ����ʱz���Ϊz=3a+11��
���� ������Ҫ�������Թ滮��Ӧ�ã��漰Ŀ�꺯���ļ������壬���ֱ�ߵĽؾ࣬������б�ʣ��Լ����빫ʽ�ǽ������Ĺؼ����ۺ��Խ�ǿ��

| A�� | C?B?A | B�� | A?B?C | C�� | C?A=B | D�� | A=B=C |
| A�� | $\frac{��}{4}$ | B�� | $\frac{��}{4}$��$\frac{5��}{4}$ | C�� | 2k��+$\frac{��}{4}$��k��Z�� | D�� | k��+$\frac{��}{4}$��k��Z�� |
| A�� | m������ | |
| B�� | m������ | |
| C�� | ��d��0ʱ��m��Ϊ��������d��0ʱ��m��Ϊ���� | |
| D�� | ��d��0ʱ��m��Ϊ��������d��0ʱ��m��Ϊ���� |