题目内容
16.设$\overrightarrow{a}$=(1,2,0),$\overrightarrow{b}$=(1,0,1).则“$\overrightarrow{c}$=($\frac{2}{3}$,-$\frac{1}{3}$,-$\frac{2}{3}$)”是“$\overrightarrow{c}$⊥$\overrightarrow{a}$,$\overrightarrow{c}$⊥$\overrightarrow{b}$且$\overrightarrow{c}$为单位向量”的充分不必要条件(填充要,充分不必要,必要不充分).分析 根据向量数量积的定义和公式求出$\overrightarrow{c}$的坐标,根据充分条件和必要条件的定义进行判断即可.
解答 解:设$\overrightarrow{c}$=(x,y,z),若满足“$\overrightarrow{c}$⊥$\overrightarrow{a}$,$\overrightarrow{c}$⊥$\overrightarrow{b}$且$\overrightarrow{c}$为单位向量”
则$\left\{\begin{array}{l}{\overrightarrow{c}•\overrightarrow{a}=x+2y=0}\\{\overrightarrow{c}•\overrightarrow{b}=x+z=0}\\{{x}^{2}+{y}^{2}+{z}^{2}=1}\end{array}\right.$,
即x=-2y,z=-x=2y,代入x2+y2+z2=1得4y2+y2+4y2=1,
即9y2=1,y2=$\frac{1}{9}$,
则y=$\frac{1}{3}$或$-\frac{1}{3}$,
当y=$\frac{1}{3}$时,$\overrightarrow{c}$=(-$\frac{2}{3}$,$\frac{1}{3}$,$\frac{2}{3}$),
当y=$-\frac{1}{3}$,$\overrightarrow{c}$=($\frac{2}{3}$,-$\frac{1}{3}$,-$\frac{2}{3}$),
故“$\overrightarrow{c}$=($\frac{2}{3}$,-$\frac{1}{3}$,-$\frac{2}{3}$)”是“$\overrightarrow{c}$⊥$\overrightarrow{a}$,$\overrightarrow{c}$⊥$\overrightarrow{b}$且$\overrightarrow{c}$为单位向量”的充分不必要条件,
故答案为:充分不必要
点评 本题主要考查充分条件和必要条件的判断,根据向量数量积的定义求出向量$\overrightarrow{c}$的坐标是解决本题的关键.

| A. | $\frac{21}{2}$ | B. | $\frac{15}{4}$ | C. | 10 | D. | 5 |
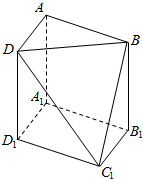 在如图所示的几何体ABD-A1B1C1D1中,底面A1B1C1D1是矩形,AA1⊥平面A1B1C1D1,且AA1平行且等于BB1平行且等于DD1,若∠DC1D1=-$\frac{π}{4}$,∠BC1B1=$\frac{π}{3}$,BC1=2,则该几何体的体积是( )
在如图所示的几何体ABD-A1B1C1D1中,底面A1B1C1D1是矩形,AA1⊥平面A1B1C1D1,且AA1平行且等于BB1平行且等于DD1,若∠DC1D1=-$\frac{π}{4}$,∠BC1B1=$\frac{π}{3}$,BC1=2,则该几何体的体积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{8}{3}$ | D. | $\frac{5}{2}$ |