题目内容
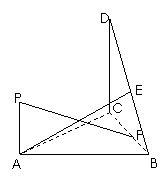
如图,直角三角形BCD所在的平面垂直于正三角形ABC所在的平面,其中
,
平面ABC, DC=BC=2PA , E．F分别为DB．CB的中点．（1）证明：AE
BC；
（2）求直线PF与平面BCD所成的角．
证明：（１）可证
，所以
平面ＡＥＦ，则AEBC；
 |
（２）可证
即为直线PF与平面BCD所成的角．
在
中，因为
，
所以
，故＝
．即直线PF与平面BCD所成的角为．
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案
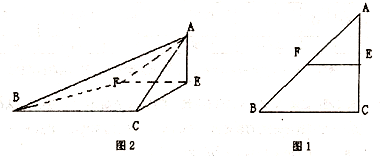已知△ABC是腰长为2的等腰直角三角形（如图1），∠BCA=90°，在边AC、AB上分别取点E、F、，使得EF∥BC，把△AEF沿直线EF折起，使∠AEC=90°，得四棱锥A-ECBF（如图2）．在四棱锥A-ECBF中，
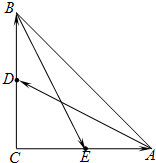如图，三角形ABC是直角三角形，C=90°，边AC、BC的中点分别是E、D，若
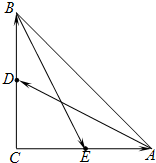如图，三角形ABC是直角三角形，C=90°，边AC、BC的中点分别是E、D，若
，
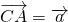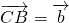，且
=2.0
、
表示
和
；