Question

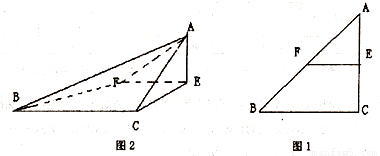
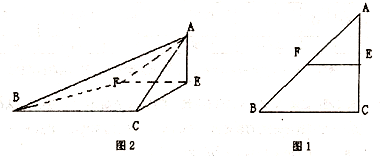已知△ABC是腰长为2的等腰直角三角形（如图1），∠BCA=90°，在边AC、AB上分别取点E、F、，使得EF∥BC，把△AEF沿直线EF折起，使∠AEC=90°，得四棱锥A-ECBF（如图2）．在四棱锥A-ECBF中，
（I）求证：CE⊥AF； 
（II）当AE=EC时，试在AB上确定一点G，使得GF∥面AEC，并证明你的结论．

Answer 1

分析：（I）利用线面垂直的判定定理，证明CE⊥面AEF，从而可得CE⊥AF； 
（II）取AB中点G，利用线面平行的判定定理，可得GF∥面AEC．

解答：（Ⅰ）证明：∵△ABC中，∠BCA=90°，且EF∥BC，∴EF⊥CE
又∵∠AEC=90°，∴CE⊥AE，
又∵AE∩EF=E，AE、EF?面AEF
∴CE⊥面AEF
∵AF?面AEF，
∴CE⊥AF…（8分）
（Ⅱ）解：取AB中点G，可得GF∥面AEC…（9分）
证明如下：取AC中点M，连结GF、EM、GM，
∵AF=FB，EC=EA，∴EF∥BC，EF=

1

2

BC
∵G、M分别是AB、AC的中点，GM∥BC，GM=

1

2

BC
∴EF∥GM，EF=GM，
∴四边形EFGM是平行四边形，
∴GF∥EM
∴GF?面AEC，EM?面AEC，
∴GF∥面AEC…（13分）

点评：本题考查线面垂直的判定与性质，考查线面平行，考查学生分析解决问题的能力，属于中档题．