题目内容
4.已知公差不为零的等差数列{an}的首项为2,前n项和为Sn,且数列{$\frac{{S}_{n}}{{a}_{n}}$}是等差数列,求数列{an}的通项公式.分析 设等差数列{an}的公差为d,可得:an,Sn,可得$\frac{{S}_{n}}{{a}_{n}}$=$\frac{\frac{1}{2}d{n}^{2}+(2-\frac{d}{2})n}{nd+2-d}$,则$\frac{{S}_{1}}{{a}_{1}}$=1,$\frac{{S}_{2}}{{a}_{2}}$=1+$\frac{2}{d+2}$,$\frac{{S}_{3}}{{a}_{3}}$=$\frac{3d+6}{2d+2}$.利用数列{$\frac{{S}_{n}}{{a}_{n}}$}是等差数列,可得2(1+$\frac{2}{d+2}$)=1+$\frac{3d+6}{2d+2}$.解出即可得出.
解答 解:设等差数列{an}的公差为d,
∴an=2+(n-1)d,Sn=2n+$\frac{n(n-1)}{2}$d,
∴$\frac{{S}_{n}}{{a}_{n}}$=$\frac{\frac{1}{2}d{n}^{2}+(2-\frac{d}{2})n}{nd+2-d}$,
则$\frac{{S}_{1}}{{a}_{1}}$=1,$\frac{{S}_{2}}{{a}_{2}}$=$\frac{2d+(2-\frac{d}{2})×2}{2d+2-d}$=$\frac{d+4}{d+2}$=1+$\frac{2}{d+2}$.
$\frac{{S}_{3}}{{a}_{3}}$=$\frac{\frac{9}{2}d+(2-\frac{d}{2})×3}{3d+2-d}$=$\frac{3d+6}{2d+2}$.
∵数列{$\frac{{S}_{n}}{{a}_{n}}$}是等差数列,
∴2(1+$\frac{2}{d+2}$)=1+$\frac{3d+6}{2d+2}$.
解得d=2.
∴an=2+2(n-1)=2n.
点评 本题考查了等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案| A. | -sin2x | B. | sin2x | C. | -cos2x | D. | cos2x |
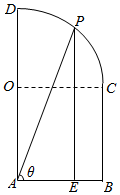 已知$\widehat{CD}$是以O为圆心,以1为半径的四分之一圆,四边形OABC为正方形,P为$\widehat{CD}$上一动点,PE⊥AB于E.
已知$\widehat{CD}$是以O为圆心,以1为半径的四分之一圆,四边形OABC为正方形,P为$\widehat{CD}$上一动点,PE⊥AB于E.