题目内容

17．某学校三个社团的人员分布如下表（每名同学只参加一个社团）
围棋社戏剧社书法社
高中4530a
初中151020
学校要对这三个社团的活动效果进行抽样调查，按分层抽样的方法从社团成员中抽取30人，结果围棋社被抽出12人．则这三个社团共有（　　）
A．130人B．140人C．150人D．160人

分析 根据围棋社共有60人，按分层抽样的方法从社团成员中抽取30人，结果围棋社被抽出12人，得到三个社团的总人数．

解答 解：：（I）围棋社共有60人，
由$\frac{45+15}{12}$×30=150，可知三个社团一共有150人，
故选：C．

点评 本题主要考查分层抽样的定义和方法，属于基础题．

练习册系列答案
相关题目
7．给出下列五种说法：
（1）函数y=ax（a＞0，a≠1）与函数y=x2的定义域相同；
（2）函数y=$\sqrt{x}$与函数y=lnx的值域相同；
（3）函数y=log3（x2-2x-3）的单调增区间是[1，+∞）；
（4）函数y=$\frac{1}{2}+\frac{1}{{{2^x}-1}}$与y=$\frac{{{{（1+{2^x}）}^2}}}{{x•{2^x}}}$都是奇函数；
（5）记函数f（x）=x-[x]（注：[x]表示不超过x的最大整数，例如：[3.2]=3，[-2.3]=-3），则f（x）的值域是[0，1）．其中所有正确的序号是（1）（4）（5）．
8．在y轴上的截距为2，且与直线y=-3x-4垂直的直线的斜截式方程为（　　）
A．$y=\frac{1}{3}x+2$B．$y=-\frac{1}{3}x-2$C．y=-3x+2D．y=3x-2
5．下列命题：
（1）y=|cos（2x+$\frac{π}{6}$）|最小正周期为π；
（2）函数y=tan$\frac{x}{2}$的图象的对称中心是（kπ，0），k∈Z；
（3）f（x）=tanx-sinx在（-$\frac{π}{2}$，$\frac{π}{2}$）上有3个零点；
（4）若$\overrightarrow{a}$∥$\overrightarrow{b}$，$\overrightarrow{b}∥\overrightarrow{c}$，则$\overrightarrow{a}∥\overrightarrow{c}$
其中错误的是（1）（3）（4）．
12．用最小二乘法计算利润额y对销售额x的回归直线方程，当销售额为4（千万元）时，估计利润额的大小（　　）
商店名称ABCDE
销售额x（千万元）35679
利润额y（百万元）23345
A．2.3B．3.2C．4.2D．2.4
2．直线l过点P（-1，2）且与以点M（-3，-2）、N（4，0）为端点的线段恒相交，则l的斜率取值范围是（　　）
A．[-$\frac{2}{5}$，5]B．[-$\frac{2}{5}$，0）∪（0，2]C．（-∞，-$\frac{2}{5}$]∪[5，+∞）D．（-∞，-$\frac{2}{5}$]∪[2，+∞）
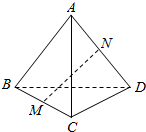9．如图，在四面体ABCD，AB=CD，M，N分别是BC，AD的中点，若AB与CD所成的角的大小为60°，则MN和CD所成的角的大小为30°或60°．
6．化简求值：已知α为第三象限角，且$cos（α-\frac{π}{2}）=-\frac{1}{5}$，求$\frac{sin（2π-α）cos（π+α）tan（π-α）}{tan（π+α）sin（π-α）}$的值．
7．在△ABC中，已知AB=4，AC=7，BC=9，则边BC上的中线长为$\frac{7}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网