题目内容
7.在△ABC中,已知AB=4,AC=7,BC=9,则边BC上的中线长为$\frac{7}{2}$.分析 △ABC中,由条件利用余弦定理求得cosB的值,△ABD中,再由余弦定理求得中线AD的值.
解答 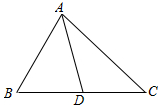 解:如图,
解:如图,
△ABC中,已知AB=4,AC=7,BC=9,设BC的中点为D,则AD为BC边上的中线长.
△ABC中,由余弦定理可得cosB=$\frac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB•BC}$=$\frac{16+81-49}{2×4×9}$=$\frac{2}{3}$.
△ABD中,由余弦定理可得AD2=AB2+BD2-2AB•BD•cosB=16+$(\frac{9}{2})^{2}$-2×$4×\frac{9}{2}×\frac{2}{3}$=$\frac{49}{4}$,
∴BD=$\frac{7}{2}$.
故答案为:$\frac{7}{2}$.
点评 本题主要考查余弦定理的应用,属于基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
17.某学校三个社团的人员分布如下表(每名同学只参加一个社团)
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从社团成员中抽取30人,结果围棋社被抽出12人.则这三个社团共有( )
| 围棋社 | 戏剧社 | 书法社 | |
| 高中 | 45 | 30 | a |
| 初中 | 15 | 10 | 20 |
| A. | 130人 | B. | 140人 | C. | 150人 | D. | 160人 |
15.记集合M={(x,y)|(x-2cosθ)2+(y-2sinθ)2<1},任取点P∈M,则点P∈{(x,y)|x2+y2≤4}的概率( )
| A. | $\frac{1}{2}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{3}$ |
12.设x,y满足$\left\{\begin{array}{l}{y≥0}\\{ax+y-1≤0}\\{3x-2y-2≤0}\end{array}\right.$,若z=x2-10x+y2的最小值为-12,实数a的取值范围是( )
| A. | a$≤-\frac{1}{2}$ | B. | a$≤-\frac{3}{2}$ | C. | a$≥\frac{1}{2}$ | D. | a$<\frac{3}{2}$ |