题目内容
10．已知正四棱锥的体积是48cm3，高为4cm，则该四棱锥的侧面积是60cm2．分析 根据体积公式计算底面边长，再利用勾股定理计算斜高，最后再计算侧面积．
解答 解：设正四锥的底面边长为a，则V=$\frac{1}{3}$×a2×4=48，解得a=6，
∴四棱锥的斜高为$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴四棱锥的侧面积S侧=$\frac{1}{2}×6×5×4$=60．
故答案为：60．
点评 本题考查了棱锥的结构特征，棱锥的侧面积计算，属于中档题．
练习册系列答案
相关题目
1．已知棱长为2，各面均为等边三角形的四面体S-ABC的各顶点都在球O的球面上，则球O的表面积为（ ）
| A． | π | B． | 2π | C． | 4π | D． | 6π |
18．
如图，已知点D为三角形ABC边BC上一点，$\overrightarrow{BD}$=3$\overrightarrow{DC}$，En（n∈N*）为AC边上的一列点，满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-（3an+2）$\overrightarrow{{E}_{n}D}$，其中实数列{an}中，an＞0，a1=1，则{an}的通项公式为（ ）
如图，已知点D为三角形ABC边BC上一点，$\overrightarrow{BD}$=3$\overrightarrow{DC}$，En（n∈N*）为AC边上的一列点，满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-（3an+2）$\overrightarrow{{E}_{n}D}$，其中实数列{an}中，an＞0，a1=1，则{an}的通项公式为（ ）| A． | 3•2n-1-1 | B． | 2n-1 | C． | 3n-2 | D． | 2•3n-1-1 |
15．观察下列各式：55=3 125，56=15 625，57=78 125，…，则52017的末四位数字为（ ）
| A． | 3 125 | B． | 5 625 | C． | 8 125 | D． | 0 625 |
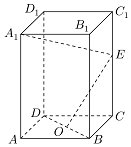如图，正四棱柱ABCD-A1B1C1D1中，O是BD的中点，E是棱CC1上任意一点．