Question

如图，已知正方形ABCD的边长为1，E在CD延长线上，且DE=CD．动点P从点A出发，沿正方形ABCD的边按逆时针方向运动一周回到A点，其中

AP

=λ

AB

+μ

AE

，则下列命题正确的是

 

．（填上所有正确命题的序号）
①λ≥0，μ≥0；
②当点P为AD中点时，λ+μ=1；
③若λ+μ=2，则点P有且只有一个；
④λ+μ的最大值为3；
⑤

AP

•

AE

的最大值为1．

Answer 1

考点：平面向量的基本定理及其意义

专题：平面向量及应用

分析：建立如图所示的直角坐标系，设正方形的边长为1，可以得到

AP

=λ

AB

+μ

AE

=（λ-μ，μ），然后根据相对应的条件加以判断即可．

解答： 解：由题意，设正方形的边长为1，建立坐标系如图，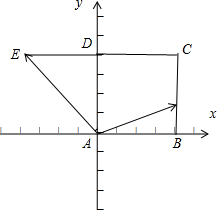
则B（1，0），E（-1，1），
∴

AB

=（1，0），

AE

（-1，1），
∵

AP

=λ

AB

+μ

AE

，
∴λ≥0，μ≥0；故①正确
∴

AP

=λ

AB

+μ

AE

=（λ-μ，μ），
当点P为AD中点时，
∴

AP

=（0，

1

2

），
∴λ-μ=0，μ=

1

2

，
故λ+μ=1；故②正确，
当λ=μ=1时，

AP

=（0，1），此时点P与D重合，满足λ+μ=2，
当λ=

3

2

，μ=

1

2

时，

AP

=（1，

1

2

），此时P是BC的中点，满足λ+μ=2，
故③错误
当P∈AB时，有0≤λ-μ≤1，μ=0，∴0≤λ≤1，0≤λ+μ≤1，
当P∈BC时，有λ-μ=1，0≤μ≤1，∴λ=μ+1，∴1≤λ≤2，∴1≤λ+μ≤3，
当P∈CD时，有0≤λ-μ≤1，μ=1，∴μ≤λ≤μ+1，即1≤λ≤2，∴2≤λ+μ≤3，
当P∈AD时，有λ-μ=0，0≤μ≤1，∴0≤λ≤1，∴0≤λ+μ≤2，
综上，0≤λ+μ≤3，
故④正确；

AP

•

AE

=（λ-μ，μ）•（-1，1）=-λ+2μ，有推理④的过程可知-λ+2μ的最大值为1，
综上，正确的命题是①②④⑤．
故答案：①②④⑤

点评：本题考查向量加减的几何意义，涉及分类讨论以及反例的方法，是易错题．