题目内容
设变量x,y满足
,若直线y=kx-2,(k>0)经过该可行域,则k的取值范围是 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用k的几何意义即可得到k的最值.
解答:
 解:画出
解:画出
的可行域如图,k为直线y=kx-2的斜率,直线过定点P(0,-2),
并且直线过可行域的A,B,两个临界点,
,解得A(2,-1),
解得B(-1,-1)
∴k≥kAP=
=
,∴k≤kBP=
=-1,
∴k的取值范围是(-∞,-1]∪[
,+∞)
故答案为:(-∞,-1]∪[
,+∞).
 解:画出
解:画出
|
并且直线过可行域的A,B,两个临界点,
|
|
∴k≥kAP=
| -1+2 |
| 2 |
| 1 |
| 2 |
| -1+2 |
| -1 |
∴k的取值范围是(-∞,-1]∪[
| 1 |
| 2 |
故答案为:(-∞,-1]∪[
| 1 |
| 2 |
点评:本题主要考查线性规划的应用以及直线斜率的计算,利用z的几何意义,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
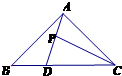 如图,在直角△ABC中,|
如图,在直角△ABC中,|| AB |
| AC |
| DC |
| BD |
| AP |
| CP |
A、[0,
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
 如图所示,AC和AB分别是圆O的切线,且OC=3,AB=4,延长AO到D点,则△ABD的面积是
如图所示,AC和AB分别是圆O的切线,且OC=3,AB=4,延长AO到D点,则△ABD的面积是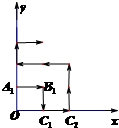 某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点A1(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么
某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点A1(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么