题目内容
8.为了得到函数y=2sin($\frac{x}{3}-\frac{π}{6}$),x∈R的图象只需把函数y=2sinx,x∈R的图象上所有的点( )| A. | 向右平移$\frac{π}{6}$个单位长度,再把所有各点的横坐标缩短到原来的$\frac{1}{3}$倍 | |
| B. | 向左平移$\frac{π}{6}$个单位长度,再把所有各点的横坐标伸长到原来的3倍 | |
| C. | 向左平移$\frac{π}{6}$个单位长度,再把所有各点的横坐标缩短到原来的$\frac{1}{3}$倍 | |
| D. | 向右平移$\frac{π}{6}$个单位长度,再把所有各点的横坐标伸长到原来的3倍 |
分析 由已知结合函数图象平移变换和伸缩变换的规律即可得答案.
解答 解:把y=2sinx的图象向右平移$\frac{π}{6}$个单位得y=2sin(x-$\frac{π}{6}$)的图象,
再把所得图象上点的纵坐标不变,横坐标扩大到原来的3倍,得y=2sin($\frac{1}{3}$x-$\frac{π}{6}$)的图象,
故选:D.
点评 本题考查y=Asin(ωx+φ)型函数的图象变换,是基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
16.已知函数f(x)=-sin(x+$\frac{π}{2}$),(x∈R),下面结论错误的是( )
| A. | 函数f(x)的最小正周期为2π | B. | 函数f(x)在区间[0,$\frac{π}{2}$]上是增函数 | ||
| C. | 函数f(x)的图象关于直线x=0对称 | D. | 函数f(x)是奇函数 |
13.函数y=x2cos x在x=1处的导数是( )
| A. | 0 | B. | 2cos1-sin 1 | C. | cos1-sin 1 | D. | 1 |
20.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的离心率为$\frac{{\sqrt{6}}}{2}$,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
17.如图所示是正三棱锥V-ABC的正视图,侧视图和俯视图,则其正视图的面积为( ) 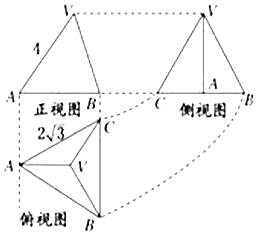

| A. | 6 | B. | 5 | C. | 4$\sqrt{3}$ | D. | 3$\sqrt{3}$ |