题目内容
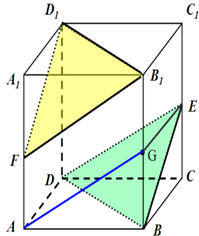
已知，在正方体ABCD-A1B1C1D1中，E、F分别是CC1、AA1的中点，求证：平面BDE∥平面B1D1F．
考点：平面与平面平行的判定
专题：空间位置关系与距离
分析：根据面面平行的判定定理即可得到结论．
解答：
解：在正方体ABCD-A1B1C1D1中，BD∥B1D1，
∵E、F分别是CC1、AA1的中点，
∴连结AG，（G为B1B的中点），DE，
则四边形ADEG为平行四边形，
∴B1F∥AG∥DE，
∵D1F∩D1B1=D1，
∴根据面面平行的推论可知，平面BDE∥平面B1D1F．
∵E、F分别是CC1、AA1的中点，
∴连结AG，（G为B1B的中点），DE，
则四边形ADEG为平行四边形，
∴B1F∥AG∥DE，
∵D1F∩D1B1=D1，
∴根据面面平行的推论可知，平面BDE∥平面B1D1F．
点评：本题主要考查面面平行的判断，根据面面平行的判定转化为直线与直线平行是解决本题的关键，要求熟练掌握相应的判定定理．
练习册系列答案
相关题目
如图，现要在边长为100m的正方形ABCD内建一个交通“环岛”．以正方形的四个顶点为圆心在四个角分别建半径为xm（x不小于9）的扇形花坛，以正方形的中心为圆心建一个半径为