题目内容
8.己知正方体ABCD-A1B1C1D1中,E为BC的中点,求异面直线A1C、DE所成角的余弦值.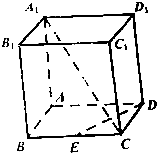
分析 以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角系,利用向量法能求出异面直线A1C、DE所成角的余弦值.
解答 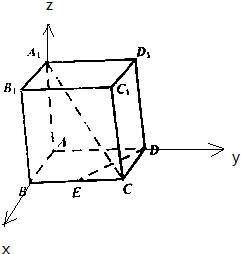 解:以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角系,设正方体ABCD-A1B1C1D1中棱长为2,
解:以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角系,设正方体ABCD-A1B1C1D1中棱长为2,
则A1(0,0,2),C(2,2,0),D(0,2,0),E(2,1,0),
$\overrightarrow{{A}_{1}C}$=(2,2,-2),$\overrightarrow{DE}$=(2,-1,0),
设异面直线A1C、DE所成角为θ,
则cosθ=$\frac{|\overrightarrow{{A}_{1}C}•\overrightarrow{DE}|}{|\overrightarrow{{A}_{1}C}|•|\overrightarrow{DE}|}$=$\frac{2}{\sqrt{12}•\sqrt{5}}$=$\frac{\sqrt{15}}{15}$.
∴异面直线A1C、DE所成角的余弦值为$\frac{\sqrt{15}}{15}$.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
16.已知函数f(x)=-2x2-kx+8在区间[1,2]上是单调函数,则k的取值范围是( )
| A. | (-∞,-8] | B. | [-8,-4] | C. | (-∞,4]∪[8,+∞) | D. | (-∞,-8]∪[-4,+∞) |
13.已知集合M={x|y=$\frac{1}{\sqrt{4-2x}}$+1},集合N={y|y=-x2+4x-2},则集合M与集合N的关系为( )
| A. | M?N | B. | M?N | C. | M=N | D. | M?N |
2.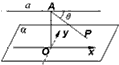 如图,已知直线a∥平面α,在平面α内有一动点P,点A是定直线a上定点,且AP与a所成角为θ(θ为锐角),点A到平面α距离为d,则动点P的轨迹方程为( )
如图,已知直线a∥平面α,在平面α内有一动点P,点A是定直线a上定点,且AP与a所成角为θ(θ为锐角),点A到平面α距离为d,则动点P的轨迹方程为( )
 如图,已知直线a∥平面α,在平面α内有一动点P,点A是定直线a上定点,且AP与a所成角为θ(θ为锐角),点A到平面α距离为d,则动点P的轨迹方程为( )
如图,已知直线a∥平面α,在平面α内有一动点P,点A是定直线a上定点,且AP与a所成角为θ(θ为锐角),点A到平面α距离为d,则动点P的轨迹方程为( )| A. | tan2θx2+y2=d2 | B. | tan2θx2-y2=d2 | C. | ${y^2}=2d(x-\frac{d}{tanθ})$ | D. | ${y^2}=-2d(x-\frac{d}{tanθ})$ |