题目内容
5.已知f(x)=sinx+log2$\frac{1+x}{1-x}$+1.(1)求f($\frac{1}{2}$)+f(-$\frac{1}{2}$)的值;
(2)若f(sinθ)>f(cosθ),θ为锐角,求θ的取值范围.
分析 (1)直接利用函数的解析式求解函数值即可.
(2)利用函数的单调性,转化不等式求解即可.
解答 解:(1)f(x)=sinx+log2$\frac{1+x}{1-x}$+1.
f($\frac{1}{2}$)+f(-$\frac{1}{2}$)=sin$\frac{1}{2}$+log2$\frac{1+\frac{1}{2}}{1-\frac{1}{2}}$+1+sin(-$\frac{1}{2}$)+log2$\frac{1-\frac{1}{2}}{1+\frac{1}{2}}$+1=2.
(2)f(x)=sinx+log2$\frac{1+x}{1-x}$+1,x∈(-1,1)函数是增函数,
f(sinθ)>f(cosθ),θ为锐角,
可得sinθ>cosθ,
可得θ∈($\frac{π}{4}$,$\frac{π}{2}$).
点评 本题考查函数的单调性的应用,函数值的求法,考查计算能力.

练习册系列答案
相关题目
10.已知x,y满足约束条件$\left\{\begin{array}{l}{2y-x-1≥0}\\{2y-3x+1≤0}\\{2y+x-11≤0}\end{array}\right.$,z=ax+by(a>b>0)最大值为12,则$\frac{5}{a}$+$\frac{2}{b}$的最小值为( )
| A. | $\frac{31+10\sqrt{6}}{12}$ | B. | $\frac{23+4\sqrt{30}}{12}$ | C. | $\frac{7+2\sqrt{10}}{12}$ | D. | 4 |
20.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的函数为( )
| A. | y=x-1 | B. | y=(x+1)2 | C. | f(x)=4x2-mx+5 | D. | y=x2 |
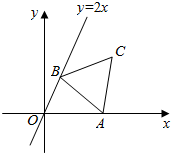 如图,在x轴上有动点A,直线y=2x上有动点B,定点C(4,3),当△ABC的周长最小时,求A,B两点的坐标.
如图,在x轴上有动点A,直线y=2x上有动点B,定点C(4,3),当△ABC的周长最小时,求A,B两点的坐标.