题目内容
极坐标系的极点是直角坐标系的原点，极轴为
轴正半轴．已知曲线
的极坐标方程为
，曲线
的参数方程为
（其中
为参数）
（1）求曲线
的直角坐标方程和曲线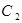
的普通方程；
（2）判断曲线和曲线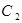的位置关系；若曲线和曲线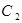相交，求出弦长．
（1）：
,
;（2）
解析试题分析：（1）利用极坐标系中点转化为直角坐标系中的点的方法可求得C1:
,C2: ；（2）利用点到直线的距离公式可求得d=
=
,然后再求弦长．
试题解析：（1）由得
，所以，
即曲线： 3分
由得，
， 5分
即曲线 6分;
（2）由（1）得，圆的圆心为（2,0），半径为2， 7分
圆心到直线的距离为
8分
所以曲线和曲线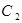的相交 9分
所求弦长为： 13分．
考点：1,极坐标系中点转为直坐标系中的点的方法2，点到直线的距离．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
：
（
为参数），
：
（
为参数）．
对应的参数为
，
为
中点
到直线
：
（
（α为参数）已知在极坐标（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，点P的极坐标为（4，
），判断点P与直线l的位置关系；
ρ·cos
＋6＝0.
，
.
垂直，根据（1）中你得到的参数方程，确定D的坐标.
的极坐标方程为
，直线
的参数方程为
为参数），点
的极坐标为
，设直线
.
的值. 
（t为参数，0≤α<π）。以原点为极点，x轴的正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为
，求α的值。
化为直角坐标方程 .
为直角坐标方程:_ ▲ .