题目内容
已知双曲线C1:
-y2=1的两条渐近线方程分别为l1,l2,A,B分别为l1,l2上的两点,|AB|=
,且动点P满足
=
+
.
(Ⅰ)求点P的轨迹方程C2;
(Ⅱ)过点S(0,-
)且斜率为k的动直线l交曲线C2于E,F两点,在y轴上是否存在定点M,使以EF为直径的圆恒过这个点?若存在,求出M的坐标;若不存在,说明理由.
| x2 |
| 2 |
| 2 |
| OP |
| OA |
| OB |
(Ⅰ)求点P的轨迹方程C2;
(Ⅱ)过点S(0,-
| 3 |
| 5 |
考点:直线与圆锥曲线的综合问题,双曲线的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(I)双曲线C1:
-y2=1的两条渐近线方程分别为l1:y=
x;l2:y=-
x.由于A,B分别为l1,l2上的两点,设A(x1,y1),B(x2,y2).则y1=
x1,y2=-
x2.设P(x,y),由于动点P满足
=
+
,可得x=x1+x2,y=y1+y2=
(x1-x2).利用|AB|=
,可得
=
.即(x1-x2)2+
(x1+x2)2=2,即可得出.
(II)设E(x3,y3),F(x4,y4).过点S(0,-
)且斜率为k的动直线l的方程为:y=kx-
.与椭圆方程联立可得根与系数的关系,假设在y轴上存在定点M(0,m),使以EF为直径的圆恒过这个点.则
•
=0.再利用数量积运算即可得出.
| x2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| OP |
| OA |
| OB |
| ||
| 2 |
| 2 |
| (x1-x2)2+(y1-y2)2 |
| 2 |
| 1 |
| 2 |
(II)设E(x3,y3),F(x4,y4).过点S(0,-
| 3 |
| 5 |
| 3 |
| 5 |
| ME |
| MF |
解答:
解:(I)双曲线C1:
-y2=1的两条渐近线方程分别为l1:y=
x;l2:y=-
x.
∵A,B分别为l1,l2上的两点,设A(x1,y1),B(x2,y2).则y1=
x1,y2=-
x2.
设P(x,y),∵动点P满足
=
+
,∴(x,y)=(x1+x2,y1+y2).
∴x=x1+x2,y=y1+y2=
(x1-x2).
∵|AB|=
,∴
=
.
∴(x1-x2)2+
(x1+x2)2=2,
∴2y2+
x2=2,
化为
+y2=1,即为点P的轨迹方程C2;
(II)设E(x3,y3),F(x4,y4).
过点S(0,-
)且斜率为k的动直线l的方程为:y=kx-
.
联立
,化为(25+100k2)x2-120kx-64=0.
∴x3+x4=
,x3x4=
.
y3y4=(kx3-
)(kx4-
)=k2x3x4-
k(x3+x4)+
.
y3+y4=k(x3+x4)-
.
假设在y轴上存在定点M(0,m),使以EF为直径的圆恒过这个点.
则
•
=0.
∴(x3,y3-m)•(x4,y4-m)=x3x4+(y3-m)(y4-m)=x3x4+y3y4-m(y3+y4)+m2=0.
∴(1+k2)x3x4-(
k+mk)(x3+x4)+
+
m+m2=0.
∴
-(
k+mk)•
+
+
m+m2=0.
化为:k2(20m2-20)+5m2+6m-11=0.
令
,解得m=1.
因此定点M(0,1),使以EF为直径的圆恒过这个点.
| x2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∵A,B分别为l1,l2上的两点,设A(x1,y1),B(x2,y2).则y1=
| ||
| 2 |
| ||
| 2 |
设P(x,y),∵动点P满足
| OP |
| OA |
| OB |
∴x=x1+x2,y=y1+y2=
| ||
| 2 |
∵|AB|=
| 2 |
| (x1-x2)2+(y1-y2)2 |
| 2 |
∴(x1-x2)2+
| 1 |
| 2 |
∴2y2+
| 1 |
| 2 |
化为
| x2 |
| 4 |
(II)设E(x3,y3),F(x4,y4).
过点S(0,-
| 3 |
| 5 |
| 3 |
| 5 |
联立
|
∴x3+x4=
| 120k |
| 25+100k2 |
| -64 |
| 25+100k2 |
y3y4=(kx3-
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 9 |
| 25 |
y3+y4=k(x3+x4)-
| 6 |
| 5 |
假设在y轴上存在定点M(0,m),使以EF为直径的圆恒过这个点.
则
| ME |
| MF |
∴(x3,y3-m)•(x4,y4-m)=x3x4+(y3-m)(y4-m)=x3x4+y3y4-m(y3+y4)+m2=0.
∴(1+k2)x3x4-(
| 3 |
| 5 |
| 9 |
| 25 |
| 6 |
| 5 |
∴
| -64(1+k2) |
| 25+100k2 |
| 3 |
| 5 |
| 120k |
| 25+100k2 |
| 9 |
| 25 |
| 6 |
| 5 |
化为:k2(20m2-20)+5m2+6m-11=0.
令
|
因此定点M(0,1),使以EF为直径的圆恒过这个点.
点评:本题考查了双曲线与椭圆的标准方程及其性质、直线与椭圆相交转化为方程联立得到根与系数的关系、圆的性质、向量的坐标运算、数量积运算等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
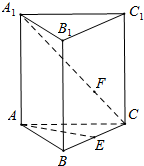 如图,已知正三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,动点F在线段CA1上,且不与点C、A1重合.
如图,已知正三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,动点F在线段CA1上,且不与点C、A1重合.