Question

6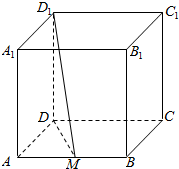．如图所示，正方体ABCD-A₁B₁C₁D₁的棱长为1，M是AB的中点，求D₁M与面ABCD所成角的正切值．

Answer 1

分析 先作出直线D₁M与平面ABCD所成角，然后求解即可；

解答 解：连接DM，因为几何体是正方体，
所以∠D₁MD就是直线D₁M与平面ABCD所成角，
正方体ABCD-A₁B₁C₁D₁的棱长为1，M是AB的中点，
DM=$\sqrt{1+\frac{1}{4}}$=$\frac{\sqrt{5}}{2}$
tan∠D₁MD=$\frac{{DD}_{1}}{DM}$=$\frac{1}{\frac{\sqrt{5}}{2}}$=$\frac{2\sqrt{5}}{5}$．

点评 本题考查正方体的几何特征，直线与平面所成角的求法，考查空间想象能力，是中档题．