题目内容
11.设极坐标系的极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,两个坐标系的单位相同.已知曲线C的极坐标方程为ρ=4sinθ,直线l的参数方程为$\left\{\begin{array}{l}{x=1+t}\\{y=m-2t}\end{array}\right.$(t为参数,t∈R,m∈R),若直线l与曲线C有公共点,求实数m的取值范围.分析 利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\\{{ρ}^{2}={x}^{2}+{y}^{2}}\end{array}\right.$把圆的极坐标方程化为直角标准方程,把直线l的参数方程化为普通方程,根据直线l与曲线C有公共点的充要条件是圆心C到直线l的距离d≤R,即可得出.
解答 解:曲线C的极坐标方程为ρ=4sinθ,化为ρ2=4ρsinθ,∴直角坐标方程为:x2+y2=4y,配方为:x2+(y-2)2=2,
可得圆心C(0,2),半径R=$\sqrt{2}$.
直线l的参数方程为$\left\{\begin{array}{l}{x=1+t}\\{y=m-2t}\end{array}\right.$(t为参数,t∈R),消去参数t可得2x+y-2-m=0.
∵直线l与曲线C有公共点,
∴圆心C到直线l的距离d=$\frac{|0+2-2-m|}{\sqrt{5}}$=$\frac{|m|}{\sqrt{5}}$≤$\sqrt{2}$,
解得$-\sqrt{10}$≤m≤$\sqrt{10}$.
∴实数m的取值范围是$[-\sqrt{10},\sqrt{10}]$.
点评 本题考查了极坐标方程化为直角标准方程、直线的参数方程化为普通方程、直线与圆的公共点的充要条件、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.经过三棱锥A-BCD的棱DA、CD的中点E、F和面ABC重心G的平面,与三棱锥的各面的交线形成的几何图形是( )
| A. | 三角形 | B. | 梯形 | C. | 菱形 | D. | 平面四边形 |
20.tanA+$\frac{1}{tanA}$=m,则sin2A=( )
| A. | $\frac{1}{m^2}$ | B. | $\frac{1}{m}$ | C. | 2m | D. | $\frac{2}{m}$ |
 如图所示,三棱锥P-ABC中,平面PAB⊥底面ABC,且PA=PB=PC,则△ABC是直角三角形.
如图所示,三棱锥P-ABC中,平面PAB⊥底面ABC,且PA=PB=PC,则△ABC是直角三角形.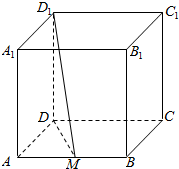 如图所示,正方体ABCD-A1B1C1D1的棱长为1,M是AB的中点,求D1M与面ABCD所成角的正切值.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,M是AB的中点,求D1M与面ABCD所成角的正切值.