题目内容
18.求过(3,1)点,且与两平行直线l1:x+2y+3=0,l2:x+2y-7=0都相切的圆的方程.分析 满足条件的圆的圆心到直线l1和l2距离相等,由此得到圆心在直线x+2y-2=0上,设出圆心坐标,得到半径,利用PC=r求出t.
解答 解:满足条件的圆的圆心到直线l1和l2距离相等,设满足条件的直线方程为x+2y+m=0,
则|m-3|=|m+7|,解得m=-2,
所以满足条件的直线方程为:x+2y-2=0;
设圆心C为(2-2t,t),且半径r=$\frac{|-2-3|}{\sqrt{5}}$=$\sqrt{5}$,
由圆过点P(3,1),所以|PC|=r,即[3-(2-2t)]2+(1-t)2=5,
解得t=-1,或t=$\frac{3}{5}$,即C($\frac{4}{5}$,$\frac{3}{5}$)或(4,-1),
所以满足条件的圆的方程为(x-$\frac{4}{5}$)2+(y-$\frac{3}{5}$)2=5或(x-4)2+(y+1)2=5.
点评 本题考查了由直线与直线,直线与圆的位置关系求满足条件的方程;根据是由位置关系得到参数的等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下面列举的图形一定是平面图形的是( )
| A. | 有一个角是直角的四边形 | B. | 有两个角是直角的四边形 | ||
| C. | 有三个角是直角的四边形 | D. | 有四个角是直角的四边形 |
10.在△ABC中,若b+c=$\sqrt{2}$+1,B=30°,C=45°,则( )
| A. | b=1,c=$\sqrt{2}$ | B. | b=$\sqrt{2}$,c=1 | C. | b=$\frac{\sqrt{2}}{2}$,c=1+$\frac{\sqrt{2}}{2}$ | D. | b=1+$\frac{\sqrt{2}}{2}$,c=$\frac{\sqrt{2}}{2}$ |
 某铝制品厂在边长为40cm的正方形铝板上割下四个半径为20厘米的圆形(如图所示的阴影部分).该厂打算用余下的部分制作底面直径和高相等的圆柱形包装盒(接缝用料忽略不计).问:
某铝制品厂在边长为40cm的正方形铝板上割下四个半径为20厘米的圆形(如图所示的阴影部分).该厂打算用余下的部分制作底面直径和高相等的圆柱形包装盒(接缝用料忽略不计).问: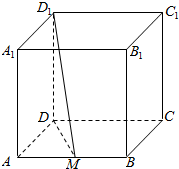 如图所示,正方体ABCD-A1B1C1D1的棱长为1,M是AB的中点,求D1M与面ABCD所成角的正切值.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,M是AB的中点,求D1M与面ABCD所成角的正切值.