题目内容
设函数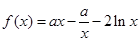 .
.
(1)若 在
在 时有极值,求实数
时有极值,求实数 的值和
的值和 的极大值;
的极大值;
(2)若 在定义域上是增函数,求实数
在定义域上是增函数,求实数 的取值范围.
的取值范围.
(1) 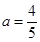 ,
, 的极大值为
的极大值为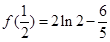 ;(2)
;(2)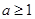 .
.
解析试题分析:(1)由函数的极值可知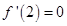 ,对函数求导
,对函数求导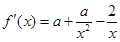 ,将2代入可得
,将2代入可得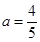 ,则有
,则有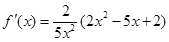 ,令
,令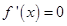 得
得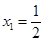 ,
,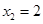 ,
, 在区间
在区间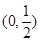 和
和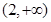 上递增,在区间
上递增,在区间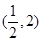 上递减,所以
上递减,所以 的极大值为
的极大值为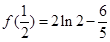 ;(2)
;(2) 在定义域上是增函数,则
在定义域上是增函数,则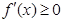 在
在 时恒成立,又
时恒成立,又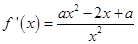 ,则需
,则需 时
时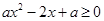 恒成立,即
恒成立,即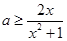 恒成立,
恒成立,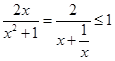 ,可得
,可得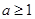 .
.
解:(1)∵ 在
在 时有极值,∴有
时有极值,∴有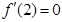
又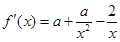 ∴
∴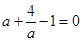 , ∴
, ∴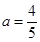 .
.
∴有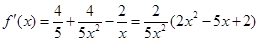
由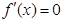 得
得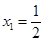 ,
,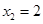
又 ∴由
∴由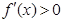 得
得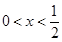 或
或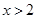
由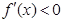 得
得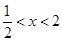
∴ 在区间
在区间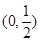 和
和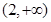 上递增,在区间
上递增,在区间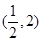 上递减
上递减
∴ 的极大值为
的极大值为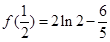
(2)若 在定义域上是增函数,则
在定义域上是增函数,则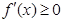 在
在 时恒成立
时恒成立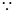
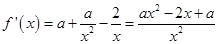 ,
,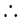 需
需 时
时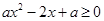 恒成立,
恒成立,
化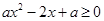 为
为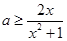 恒成立,
恒成立,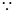
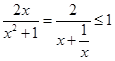 ,
, 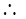
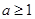 为所求.
为所求.
考点:函数的极值.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
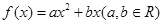 ,函数
,函数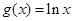 .
.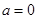 时,函数
时,函数 的图象与函数
的图象与函数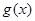 的图象有公共点,求实数
的图象有公共点,求实数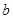 的最大值;
的最大值;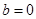 时,试判断函数
时,试判断函数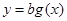 的上方?若能,求出
的上方?若能,求出 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.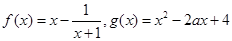 若对任意x1∈[0,1],存在x2∈[1,2],使
若对任意x1∈[0,1],存在x2∈[1,2],使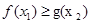 ,求实数a的取值范围?
,求实数a的取值范围?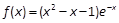 .
. 的方程f(x)=a在区间
的方程f(x)=a在区间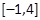 上有两个根,求a的取值范围.
上有两个根,求a的取值范围.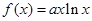
 ,已知曲线
,已知曲线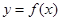 在点
在点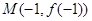 处的切线方程是
处的切线方程是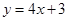 .
.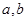 的值;并求出函数的单调区间;
的值;并求出函数的单调区间; 在区间
在区间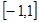 上的最值.
上的最值. ,其导函数为
,其导函数为 .
.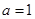 ,求函数
,求函数 在点
在点 处的切线方程;
处的切线方程;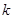 为整数,若
为整数,若 时,
时, 恒成立,试求
恒成立,试求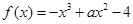 (
(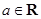 ).
).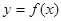 的图象在点
的图象在点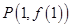 处的切线的倾斜角为
处的切线的倾斜角为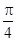 ,求
,求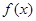 在
在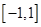 上的最小值;
上的最小值;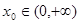 ,使
,使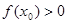 ,求
,求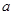 的取值范围.
的取值范围. ,曲线
,曲线 在点
在点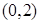 处的切线与
处的切线与 轴交点的横坐标为
轴交点的横坐标为 .
. ;
; 时,曲线
时,曲线 只有一个交点.
只有一个交点.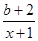 (x>1),其中b为实数.
(x>1),其中b为实数.