题目内容
已知一非零向量数列{an}满足a1=(1,1)an=(xn,yn)=
(xn-1-yn-1,xn-1+yn-1)(n≥2且n∈N*).给出以下结论:
①数列{|an|}是等差数列,②|a1|•|a5|=
;③设cn=2log2|an|,则数列{cn}的前n项和为Tn,当且仅当n=2时,Tn取得最大值;④记向量an与an-1的夹角为θn(n≥2),均有θn=
.其中所有正确结论的序号是 .
| 1 |
| 2 |
①数列{|an|}是等差数列,②|a1|•|a5|=
| 1 |
| 2 |
| π |
| 4 |
分析:利用等差数列的定义、等比数列的定义、向量的模、向量的夹角及数列的前n项和等知识对每个结论逐一判断可得答案.
解答:解:∵|an|=
=
=
|an-1|,
∴{|an|}是首项为|a1|=
,公比为q=
的等比数列,
∴①不正确.
又∵{|an|}是首项为|a1|=
,公比为q=
的等比数列,
∴|a1|•|a5|=|a1|2• q4=(
)2•(
)4=
,
∴②正确.
又∵{|an|}是首项为|a1|=
,公比为q=
的等比数列,
∴an=2•(
)n,
∴a1=
,a2=1,当n≥3时,an<1,
∴c1=1,c2=0,当n≥3时,cn<0,
∴当n=1或2时,Tn取得最大值为1,
∴③不正确.
由已知得:an-1•an=(xn-1,yn-1)•
(xn-1-yn-1,xn-1+yn-1)=
(xn-12+yn-12)=
|an-1|2,
又∵cos<an-1,an>=
,
将|an|=
|an-1|,an-1•an=
|an-1|2代入上式可得:
cos<an-1,an>=
,
∴an-1与an的夹角为θn=
,
∴④正确.
故答案为②④.
| 1 |
| 2 |
| (xn-1-yn-1)2+(xn-1+yn-1)2 |
=
| ||
| 2 |
| xn-12+yn-12 |
=
| ||
| 2 |
∴{|an|}是首项为|a1|=
| 2 |
| ||
| 2 |
∴①不正确.
又∵{|an|}是首项为|a1|=
| 2 |
| ||
| 2 |
∴|a1|•|a5|=|a1|2• q4=(
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴②正确.
又∵{|an|}是首项为|a1|=
| 2 |
| ||
| 2 |
∴an=2•(
| ||
| 2 |
∴a1=
| 2 |
∴c1=1,c2=0,当n≥3时,cn<0,
∴当n=1或2时,Tn取得最大值为1,
∴③不正确.
由已知得:an-1•an=(xn-1,yn-1)•
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵cos<an-1,an>=
| an-1•an |
| |an-1|•|an| |
将|an|=
| ||
| 2 |
| 1 |
| 2 |
cos<an-1,an>=
| ||
| 2 |
∴an-1与an的夹角为θn=
| π |
| 4 |
∴④正确.
故答案为②④.
点评:本题以向量为载体,考查等差数列、等比数列及数列前n项和等知识,这是高考考查的重点,在学习中要重点关注.

练习册系列答案
相关题目
 满足
满足

 。给出以下结论:
。给出以下结论: 是等差数列,2。
是等差数列,2。 ;3。设
;3。设 ,则数列
,则数列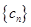 的前n项和为
的前n项和为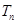 ,当且仅当n=2时,
,当且仅当n=2时, 与
与 的夹角为
的夹角为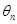 (
( ),均有
),均有 。其中所有正确结论的序号是____
。其中所有正确结论的序号是____ 满足
满足

 。给出以下结论:
。给出以下结论: 是等差数列,②
是等差数列,② ;③设
;③设 ,则数列
,则数列 的前n项和为
的前n项和为 ,当且仅当n=2时,
,当且仅当n=2时, 与
与 的夹角为
的夹角为 (
( ),均有
),均有 。其中所有正确结论的序号是_____________
。其中所有正确结论的序号是_____________