题目内容
已知A,B是椭圆 和双曲线
和双曲线 的公共顶点.过坐标原点O作一条射线与椭圆、双曲线分别交于M,N两点,直线MA,MB,NA,NB的斜率分别记为k1,k2,k3,k4,则下列关系正确的是
的公共顶点.过坐标原点O作一条射线与椭圆、双曲线分别交于M,N两点,直线MA,MB,NA,NB的斜率分别记为k1,k2,k3,k4,则下列关系正确的是
- A.k1+k2=k3+k4
- B.k1+k3=k2+k4
- C.k1+k2=-(k3+k4)
- D.k1+k3=-(k2+k4)
C
分析:设出点的坐标,求出斜率的和,利用点在曲线上,化简,即可得到结论.
解答:设M(x,y),则k1+k2= +
+ =
=
∵ ,∴
,∴ =-
=- ,∴k1+k2=-
,∴k1+k2=-
设N(x′,y′),则k3+k4= +
+ =
=
∵ ,∴
,∴ =
= ,∴k3+k4=
,∴k3+k4=
∵O,M,N共线
∴
∴k1+k2=-(k3+k4)
故选C.
点评:本题考查椭圆与双曲线的综合,考查斜率的计算,正确计算是关键.
分析:设出点的坐标,求出斜率的和,利用点在曲线上,化简,即可得到结论.
解答:设M(x,y),则k1+k2=
 +
+ =
=
∵
 ,∴
,∴ =-
=- ,∴k1+k2=-
,∴k1+k2=-
设N(x′,y′),则k3+k4=
 +
+ =
=
∵
 ,∴
,∴ =
= ,∴k3+k4=
,∴k3+k4=
∵O,M,N共线
∴

∴k1+k2=-(k3+k4)
故选C.
点评:本题考查椭圆与双曲线的综合,考查斜率的计算,正确计算是关键.

练习册系列答案
相关题目
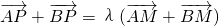 ,其中λ∈R,设直线AP、BP、AM、BM的斜率分别记为k1,k2,k3,k4,k1+k2=5,则k3+k4=________.
,其中λ∈R,设直线AP、BP、AM、BM的斜率分别记为k1,k2,k3,k4,k1+k2=5,则k3+k4=________.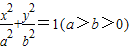 和双曲线
和双曲线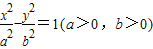 的公共顶点.P是双曲线上的动点,M是椭圆上的动点(P、M都异于A、B),且满足
的公共顶点.P是双曲线上的动点,M是椭圆上的动点(P、M都异于A、B),且满足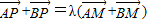 ,其中λ∈R,设直线AP、BP、AM、BM的斜率分别记为k1,k2,k3,k4,k1+k2=5,则k3+k4= .
,其中λ∈R,设直线AP、BP、AM、BM的斜率分别记为k1,k2,k3,k4,k1+k2=5,则k3+k4= . 和双曲线
和双曲线 的公共顶点.过坐标原点O作一条射线与椭圆、双曲线分别交于M,N两点,直线MA,MB,NA,NB的斜率分别记为k1,k2,k3,k4,则下列关系正确的是( )
的公共顶点.过坐标原点O作一条射线与椭圆、双曲线分别交于M,N两点,直线MA,MB,NA,NB的斜率分别记为k1,k2,k3,k4,则下列关系正确的是( )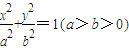 和双曲线
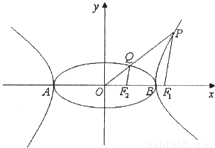
和双曲线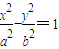 的公共顶点,P、Q分别为双曲线和椭圆上不同于A、B的动点,且
的公共顶点,P、Q分别为双曲线和椭圆上不同于A、B的动点,且 .设AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4.
.设AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4.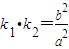 ;
;