题目内容
19.判断下列函数的奇偶性:(1)f(x)=$\sqrt{2}$sin(2x+$\frac{5}{2}$π);
(2)f(x)=$\sqrt{2sinx-1}$;
(3)f(x)=lg(sinx+$\sqrt{1+si{n}^{2}x}$)
分析 根据函数奇偶性的定义进行判断即可.
解答 解:(1)f(x)=$\sqrt{2}$sin(2x+$\frac{5}{2}$π)=$\sqrt{2}$cos2x,为偶函数;
(2)由2sinx-1≥0得sinx$≥\frac{1}{2}$,即2kπ+$\frac{π}{6}$≤x≤2kπ+$\frac{5π}{6}$,k∈Z,定义域关于原点不对称,则f(x)=$\sqrt{2sinx-1}$为非奇非偶函数;
(3)函数的定义域为(-∞,+∞),f(-x)+f(x)=lg(-sinx+$\sqrt{1+si{n}^{2}x}$)+lg(sinx+$\sqrt{1+si{n}^{2}x}$)=lg[($\sqrt{1+si{n}^{2}x}$)2-sin2x]=lg1=0,
则f(-x)=-f(x),即函数f(x)为奇函数.
点评 本题主要考查函数奇偶性的判断,根据函数奇偶性的定义结合函数定义域关于原点对称是解决本题的关键.

练习册系列答案
相关题目
11.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=4,且$\overrightarrow{a}•\overrightarrow{b}$=2$\sqrt{3}$,则$\overrightarrow{a}$与$\overrightarrow{b}$所成的角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
17.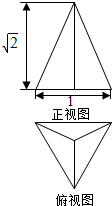 已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
 已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{4}$ | D. | $\frac{\sqrt{2}}{4}$ |
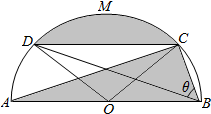 如图:阴影部分是一个机械构件.该构件是由一块半圆形铁皮剪切后,剩下了弓形面CMD,及三角形ABC所形成的.其中半圆直径AB=8,CD∥AB,点M是$\widehat{CD}$上一点,∠CBD=θ.
如图:阴影部分是一个机械构件.该构件是由一块半圆形铁皮剪切后,剩下了弓形面CMD,及三角形ABC所形成的.其中半圆直径AB=8,CD∥AB,点M是$\widehat{CD}$上一点,∠CBD=θ.