题目内容

4．已知向量$\overrightarrow{a}$=（-2，0），$\overrightarrow{b}$=（$\sqrt{3}$，1），$\overrightarrow{c}$=（lg3）$\overline{b}$，则$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为$\frac{5π}{6}$．

分析 先求出向量$\overrightarrow{c}$的坐标，然后求$cos＜\overrightarrow{a}，\overrightarrow{c}＞$，从而根据向量夹角的范围即可得出向量$\overrightarrow{a}，\overrightarrow{c}$的夹角．

解答 解：$\overrightarrow{c}=（\sqrt{3}lg3，lg3）$；
∴$cos＜\overrightarrow{a}，\overrightarrow{c}＞=\frac{\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{a}||\overrightarrow{c}|}=\frac{-2\sqrt{3}lg3}{2•2lg3}$=$-\frac{\sqrt{3}}{2}$；
∴$\overrightarrow{a}$与$\overrightarrow{c}$的夹角为$\frac{5π}{6}$．
故答案为：$\frac{5π}{6}$．

点评 考查向量坐标的数乘运算，向量夹角余弦的坐标公式，清楚向量夹角的范围，已知三角函数值求角．

练习册系列答案
相关题目
14．已知函数f（x）=ax2+（b-1）x+b+1，x∈[a，b]是偶函数．
（1）求a，b的值；
（2）在区间[-1，1]上，y=f（x）的图象恒在直线y=2x+m的图象上方，试确定实数m的范围．
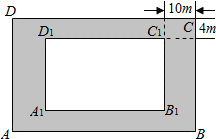15．如图，某房地产开发公司计划在一楼区内建造一个长方形公园ABCD，公园由长方形的休闲区A1B1C1D1和环公园人行道（阴影部分）组成，已知人行道的宽分别为4m和10m
（1）若休闲区A1B1C1D1的面积为4000平方米，则要使公园占地面积最小，休闲区A1B1C1D1的长和宽应如何设计？
（2）若公园的面积为4000平方米，要使休闲区A1B1C1D1的面积最大，公园的长和宽应如何设计？
12．已知函数f（x）=2ex-ax-2（a∈R）
（1）若a=2，求证：f（x）≥0．
（2）若x∈[1，2]，求f（x）的最小值．
（3）设函数y=f（x）图象上任意不同的两点A（x1，y1），B（x2，y2）且x1＜x2，记直线AB的斜率为k，求证：k＞f′（px1+qx2）（其中正常数p，q满足p+q=1且p≥q）
19．判断下列函数的奇偶性：
（1）f（x）=$\sqrt{2}$sin（2x+$\frac{5}{2}$π）；
（2）f（x）=$\sqrt{2sinx-1}$；
（3）f（x）=lg（sinx+$\sqrt{1+si{n}^{2}x}$）
9．点A（-3，6）关于点P（2，-1）对称点的点的坐标是（　　）
A．（1，-4）B．（1，4）C．（-7，8）D．（7，-8）
16．已知各项均不相等的等差数列{an}的前五项的和为S5=25，且a1，a4，a10成等比数列．
（1）求数列{an}的通项公式；
（2）记Tn为数列{$\frac{1}{{a}_{n}•{a}_{n+1}}$}的前n项和，若Tn≤λan+1对?n∈N*都成立，求实数λ的最小值．
1．（1）已知某圆圆心在x轴上，半径为5，且截y轴所得线段长为8，求该圆的标准方程．
（2）已知双曲线与椭圆$\frac{x^2}{16}$+$\frac{y^2}{49}$=1有公共的焦点，并且椭圆的离心率与双曲线的离心率之比为$\frac{3}{7}$，求双曲线的标准方程．
2．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的一条渐近线与圆（x-3）2+y2=9相交于A．B两点，若|AB|=2，则该双曲线的离心率为（　　）
A．8B．$2\sqrt{2}$C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网