题目内容
10.若函数y=f(x)=$\frac{a•{2}^{x}-1-a}{{2}^{x}-1}$为奇函数.(1)确定a的值;
(2)求函数的定义域;
(3)求函数的值域;
(4)讨论函数的单调性.
分析 (1)根据函数奇偶性的定义和性质建立方程关系即可确定a的值;
(2)根据函数出来的条件即可求函数的定义域;
(3)利用分式函数的性质结合指数函数的性质即可求函数的值域;
(4)根据指数函数单调性的性质进行讨论即可判断函数的单调性.
解答 解:(1)∵函数的定义域为(-∞,0)∪(0,+∞),
∴若f(x)为奇函数,
则f(-x)=-f(x),即$\frac{a•{2}^{-x}-1-a}{{2}^{-x}-1}$=-$\frac{a•{2}^{x}-1-a}{{2}^{x}-1}$,
即$\frac{a-{2}^{x}-a•{2}^{x}}{1-{2}^{x}}$=-$\frac{a•{2}^{x}-1-a}{{2}^{x}-1}$,
则a-2x-a•2x=a•2x-a-1,
(2a+1)=(2a+1)•2x,
则2a+1=0,则a=-$\frac{1}{2}$.
(2)由2x-1≠0得x≠0,即函数的定义域为(-∞,0)∪(0,+∞);
(3)当a=-$\frac{1}{2}$时,f(x)=$\frac{a•{2}^{x}-1-a}{{2}^{x}-1}$=$\frac{-\frac{1}{2}•{2}^{x}-1+\frac{1}{2}}{{2}^{x}-1}$=-$\frac{1}{2}•$$\frac{{2}^{x}+1}{{2}^{x}-1}$=-$\frac{1}{2}$•$\frac{{2}^{x}-1+2}{{2}^{x}-1}$=-$\frac{1}{2}$•(1+$\frac{2}{{2}^{x}-1}$)=$-\frac{1}{2}$-$\frac{1}{{2}^{x}-1}$,
∵2x-1>-1,且2x-1≠0,
∴$\frac{1}{{2}^{x}-1}$<-1或$\frac{1}{{2}^{x}-1}$>0,
则-$\frac{1}{{2}^{x}-1}$>1或-$\frac{1}{{2}^{x}-1}$<0,
即$-\frac{1}{2}$-$\frac{1}{{2}^{x}-1}$>1$-\frac{1}{2}$=$\frac{1}{2}$或$-\frac{1}{2}$-$\frac{1}{{2}^{x}-1}$<$-\frac{1}{2}$,
即函数的值域为(-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞);
(4)当x>0时,2x-1>0,且y=2x-1为增函数,则y=$\frac{1}{{2}^{x}-1}$为减函数,y=-$\frac{1}{{2}^{x}-1}$为增函数,y=$-\frac{1}{2}$-$\frac{1}{{2}^{x}-1}$为增函数,
当x<0时,2x-1<0,且y=2x-1为增函数,则y=$\frac{1}{{2}^{x}-1}$为减函数,y=-$\frac{1}{{2}^{x}-1}$为增函数,y=$-\frac{1}{2}$-$\frac{1}{{2}^{x}-1}$为增函数,
即函数的单调递增区间为(-∞,0),(0,+∞).
点评 本题主要考查综合考查函数的定义域值域,奇偶性,单调性的性质,利用分式函数的性质以及指数函数的单调性是解决本题的关键.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
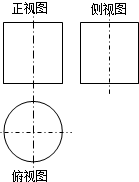 如图,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )
如图,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为( )| A. | $\frac{π}{4}$ | B. | $\frac{5}{4}π$ | C. | π | D. | $\frac{3}{2}π$ |
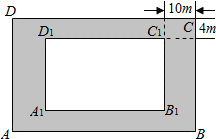 如图,某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1和环公园人行道(阴影部分)组成,已知人行道的宽分别为4m和10m
如图,某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1和环公园人行道(阴影部分)组成,已知人行道的宽分别为4m和10m