题目内容
4.求函数y=$\frac{{x}^{2}+3}{{x}^{2}+2}$的值域.分析 令t=x2(t≥0),得$g(t)=\frac{1}{t+2}+1$,然后结合t的范围得答案.
解答 解:令t=x2(t≥0),
则原函数化为g(t)=$\frac{t+3}{t+2}=\frac{t+2+1}{t+2}=\frac{1}{t+2}+1$,
由t≥0,得t+2≥2,
∴$0<\frac{1}{t+2}≤\frac{1}{2}$,则1$<\frac{1}{t+2}+1≤\frac{3}{2}$.
∴函数y=$\frac{{x}^{2}+3}{{x}^{2}+2}$的值域为(1,$\frac{3}{2}$].
点评 本题考查换元法求函数的值域,是基础的计算题.

练习册系列答案
相关题目
14.x2+y2-4y-1=0的圆心和半径分别为( )
| A. | (2,0),5 | B. | (0,-2),$\sqrt{5}$ | C. | (0,2),$\sqrt{5}$ | D. | (2,2),5 |
12.满足不等式y≤2及|x|≤y≤|x|+1所表示的平面区域的面积为( )
| A. | 2 | B. | 3 | C. | 6 | D. | 8 |
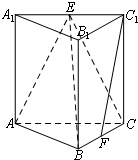 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别为A1C1、BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别为A1C1、BC的中点.