题目内容
12.满足不等式y≤2及|x|≤y≤|x|+1所表示的平面区域的面积为( )| A. | 2 | B. | 3 | C. | 6 | D. | 8 |
分析 根据题意,把原不等式化为等价的不等式组,在坐标平面内画出它表示的平面区域,求出它围成的面积即可.
解答 解:不等式y≤2及|x|≤y≤|x|+1可化为如下的两个不等式组;
①$\left\{\begin{array}{l}{x≥0}\\{y≥x}\\{y≤x+1}\\{y≤2}\end{array}\right.$,或②$\left\{\begin{array}{l}{x≤0}\\{y≥-x}\\{y≤-x+1}\\{y≤2}\end{array}\right.$;
则由不等式组①②所表示的平面区域如图所示的阴影部分,
它围成的面积为S=$\frac{1}{2}$×4×2-$\frac{1}{2}$×2×1=3.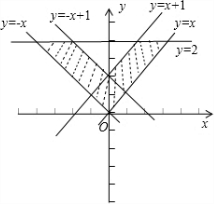
故选:B.
点评 本题考查了二元一次不等式组表示的平面区域面积的计算问题,也考查了绝对值不等式的应用问题,考查了转化思想的应用问题,是综合性题目.

练习册系列答案
相关题目
3.已知命题p:对?x∈R,x2-x-1≥0恒成立.命题q:?x∈R是2x-1≤0成立.则下列命题中为真命题的是( )
| A. | (?p)∧q | B. | (?p)∧(?q) | C. | p∧(?q) | D. | p∧q |
17.在函数y=x2-1,y=x3,y=ex,y=lnx中,奇函数是( )
| A. | y=x2-1 | B. | y=x3 | C. | y=ex | D. | y=lnx |
1.f(x)=($\frac{1}{2}$)x-x+1,用二分法求方程($\frac{1}{2}$)x-x+1=0在(0,3)内近似解的过程中,f(1)>0,f(1.5)<0,f(2)<0,f(3)<0,则方程的根落在区间( )
| A. | (1,1.5) | B. | (1.5,2) | C. | (2,3) | D. | 无法确定 |
2.cos(-30°)的值是( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |