Question

19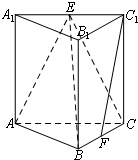．如图，在三棱柱ABC-A₁B₁C₁中，侧棱垂直于底面，AB⊥BC，E、F分别为A₁C₁、BC的中点．
（1）求证：C₁F∥平面ABE；
（2）求证：平面ABE⊥平面B₁BCC₁．

Answer 1

分析 （1）取AB中点D，连接DE，DF，运用中位线定理，可得DFC₁E为平行四边形，即有C₁F∥ED，再由线面平行的判定定理，即可得证；
（2）运用线面垂直的性质和判定，可得AB⊥面B₁BCC₁，再由面面垂直的判定定理，即可得证．

解答 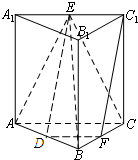证明：（1）取AB中点D，连接DE，DF，
∵D、F分别为AB、BC的中点，∴DF∥AC，且DF=$\frac{1}{2}$AC，
∵E为A₁C₁中点，∴EC₁∥AC，且EC₁=$\frac{1}{2}$AC，
∴DF∥EC₁，且DF=EC₁，
∴DFC₁E为平行四边形，∴C₁F∥ED，
又∵ED?面ABE，C₁F?面ABE，
∴C₁F∥面ABE；    
（2）∵在三棱柱ABC-A₁B₁C₁中，侧棱垂直于底面，
∴CC₁⊥面ABC，
∵AB?面ABC，∴AB⊥CC₁，
又∵AB⊥BC，BC，CC₁?面B₁BCC₁，BC∩CC₁=C，
∴AB⊥面B₁BCC₁，
∵AB?面ABE，∴面ABE⊥面B₁BCC₁．

点评 本题考查空间线面平行和面面垂直的判定定理的运用，考查空间想象能力和逻辑推理能力，属于中档题．